|
|
|
|
News The Project Technology RoboSpatium Contribute Subject index Download Responses Games Gadgets Contact <<< Eddy current Self-inductance >>> AC voltageDC VoltageAt the chapter about voltage we considered it to be a unvaried value during time. As reason for the occurrence of voltage we mentioned the potential difference inside of the electric field of a point charge.At the subsequent chapters about electric current, resistance and power we also considered voltage to be a constant value at the single components of electric networks. At the chapter about induction we have seen that the voltage generated with the help of a permanent magnet and a conductor loop is indeed not constant. In this case the voltage is called AC voltageVoltage whose polarity is alternating in regular time intervals and whose average value within one time interval is zero, is called AC voltage. The exact curve progression doesn't matter.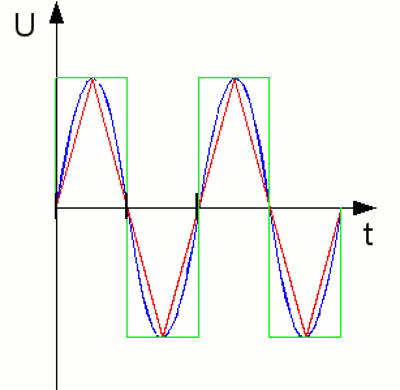
Progress of three AC voltage curves with identical time period and peak voltage: The blue curve shows a sinusoidal progress, the red curve forms triangles with the X-axis (=triangular voltage) and the green curve forms rectangles with the X-axis (=square-wave voltage). Furthermore the curves are symmetric, meaning if you flip the curve around the X-axis and move it for half a periodic time, the curve progression is identical to the original curve. TerminologyPeriod - Period is the smallest interval of time or length the values of a function are repeating.Periodic time - Periodic time (T) marks the smallest time interval possible wherein the values of the function are repeated. Where is: T - periodic time, n - integer value Frequency - Frequency (f) describes the number of periods per second. The unit for frequency is Hertz (Hz), named after the German physicist Heinrich Hertz. The correlation between frequency and periodic time is given by: Where is: f - Frequency, T - periodic time Peak to peak voltage - The peak-to-peak voltage (UPP) equals the difference between the up-most positive and negative value of the curve progression. Peak voltage - Peak voltage (UP) is the up-most value of the voltage independent from the sign of the value. Effective voltage, root mean square (RMS) - Effective voltage (Ueff) is the square root of the arithmetic mean (average) of the squares of the curve values. Using the "trick" to calculate the square root of the squares eliminates the negative sign (the square root of -12 gives +1). Expressing the condition that the average value within one periodic time becomes zero: Where is: T - periodic time, t1 - optional point of time To differentiate between DC and AC voltage, the symbol used for AC voltage is the U with a tilde as index. U˜ indicates AC voltage. 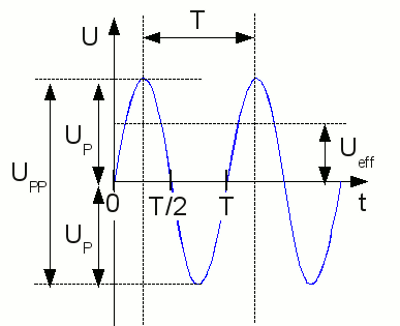
Characteristic parameters of a sinusoidal AC voltage. For the voltage progression of the (virtual) experiment with an inductor moving along a permanent magnet we get: 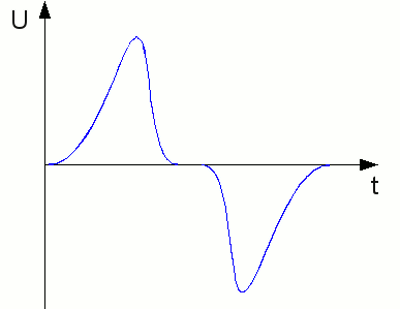
If we would restart the experiment as soon as it has ended, the result was an AC voltage, too. We will see later on, that a procedure like this is running inside of a generator. In subsequent chapters we will see, how an AC voltage can be rectified. The result gives a curve progression as follows: 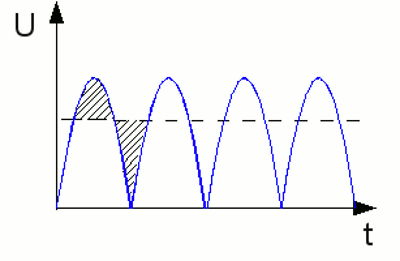
Rectified sinusoidal voltage: As per definition this is no longer an AC voltage, even though the voltage is altered periodically. No value is below zero, meaning the polarity is not altered. At the chapter about voltage, we have noticed voltage to be the energy used to move a charged particle through two points inside of an electric field. By using another basing point as reference, this kind of curve progression gives us AC voltage again (dashed line). The new base line divides the curve in a way that the areas above and below the line are equal. AC currentAs mentioned at several times before, the occurrence of voltage causes electric current. The correlation between AC voltage and the according current flowing through different linear components of an electric network will be treated some chapters later.<<< Eddy current Self-inductance >>> News The Project Technology RoboSpatium Contribute Subject index Archives Download Responses Games Links Gadgets Contact Imprint |
|
|