|
|
|
|
News The Project Technology RoboSpatium Contribute Subject index Download Responses Games Gadgets Contact Eddy currentLenz's lawAt the previous chapter we have learned how to create voltage by using a permanent magnet and an inductor. We also recognized that the thereby generated voltage altered it's sign while the coil was moving along the permanent magnet once. The direction of the field lines - crossing the loops of the coil - is decisive for the polarity of the induced voltage. If you turn around the magnet by 180 degrees, meaning the north pole points to the left and rerun the experiment, the voltmeter will point to the left at first and to the right while leaving the magnet. The polarity is contrary to the first trial. How can the polarity be predicted? Well to do this, Lenz's law is very helpful:A voltage induced by the change of a magnetic flux through a conductor loop generates a current in such a direction that the current running through the loop opposes the change of the magnetic flux causing the voltage. The law is named after the Russian-German-Estonian physicist Heinrich Lenz. Let's pick this law into pieces: 1.) A changing magnetic flux induces voltage. That's what we have seen at the previous chapter. We did so in praxis by moving an inductor (=3 inductor loops) towards a permanent magnet. 2.) The induces voltage causes a current flow through the conductor loop. That's what we inhibited by cutting the loop to interconnect a voltmeter. Let's take the voltmeter out of the circle and reconnect the ends of the loop. A voltage between two points of an conductor causes the flow of an electric current. A current is running through the coil as soon as it is moved to the permanent magnet. What's the direction of the current caused by the induced voltage? 3.) The current running through the coil causes a magnetic field as seen at the chapters inductor and magnetism. At the chapter about magnetism we have learned the "right hand grip rule". You can find out the direction of the magnetic field lines when knowing the direction of the (conventional) current. Vice versa you can find out the direction of the current when knowing the direction of the magnetic field lines. We can predict the direction of the magnetic field lines by using Lenz's law: The field lines of the induced current try to avoid or at least lessen the increase of the magnetic flux running through the loop! 
Let's have a look at a ring shaped conductor who is moving towards or away from a permanent magnet. The following drawings are based on the left picture, viewed at the x-y-plane. 
At this drawing, the permanent magnet is moved towards the conductor loop. The field lines of a permanent magnet are running from the north to the south pole (outsides the magnet). Because of the movement, more and more field lines enter the loop at the right and leave it at the left side. Based on Lenz's law a magnetic field is created, whose field lines are trying to lessen the number of field lines entering the loop. The field lines of a current through a conductor run in concentric circles around the conductor. To lessen the field of the permanent magnet, the field lines of the induced current must run from the left to the right (contrary to those of the permanent magnet) inside of the conductor loop. The appropriate direction of the (conventional) direction of the current can be identified using the "right hand grip rule". If you grip the conductor loop with your right hand in such a way that the fingers of your hand are pointing into the direction of the field lines, your thumb points into the direction of the current. In the case drawn at the picture, the current has to exit your computer screen at the upper half of the drawing (symbolized arrow seen from front, point) and the current enters the computer screen at the lower half of the drawing (symbolized arrow seen from behind, cross).. 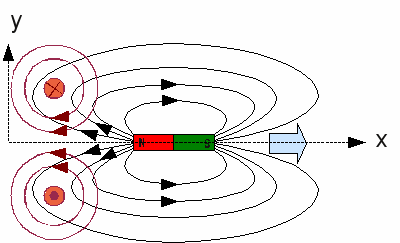
Let's move the permanent magnet to the right, away from the coil. Accordant there are running fewer field lines from right to the left through the conductor loop. The induced voltage causes a current trying to enforce the magnetic flux of the permanent magnet which becomes weakened. To do so, the field lines must run from the right to the left inside of the loop. Using the right hand grip rule the current is entering the computer screen at the upper half and exits at the lower half of the drawing. The flow of the current is contrary to those of the first case mentioned. Now you should be able to find out the direction of the current while the south pole of the permanent magnet is moved towards the conductor loop. From ring to panel
Inside of a conducting wire being bent to a ring, a circulating current is induced as soon as the magnetic flux running through it varies. How "thick" may the ring at the utmost become to generate a circulating current? And what happens to panels not being ringlike? The answer is: The shape of the conductor material doesn't matter - induced currents are always running through the material. You can imagine that as follows: 
Let's consider a rectangle shaped conductor, being penetrated by a varying, homogeneous magnetic field. Homogeneous means that the magnetic flux density has the same value at every point inside of the field. At the drawing the field lines are entering your computer screen perpendicularly pointing away from you. The magnetic flux density is lowered by now (like a permanent magnet with it's north pole pointing to the screen was moved away from your computer). Following Lenz's law, everywhere inside of the conductor small circulating currents are generated running clockwise. Let's have a closer look at the currents moving in small circles. The circles inside of the conductor are "grinding" at each other. The neighbors of a circulating current always point into the opposite direction of itself. The current is "annihilated" by it's neighbors. The voltages inducing circular currents are added up to zero at the inside of the conductor panel. No voltage means no current! The annihilation of the voltage at the boundary areas is not complete, because there are some neighbors missing. The result is a "circular" current running along the edges of the plate. This is a very academic example. Generating a completely homogeneous magnetic field requires a very complex mechanical equipment. In normal case there are always inhomogeneous flux density allocations, meaning there won't be well defined areas with or without currents running. The pattern is more like swirling water surface. That's why the induced current inside of three-dimensional conductors is called eddy current. News The Project Technology RoboSpatium Contribute Subject index Archives Download Responses Games Links Gadgets Contact Imprint |
|
|