|
|
|
|
News The Project Technology RoboSpatium Contribute Subject index Download Responses Games Gadgets Contact <<< Resistance network Inductors >>> MagnetismMagnetic fieldsThe quantum mechanical processes causing magnetic fields, should not be treated at this chapter. Let's just have a look at the phenomena around magnetic fields.The magnetic flux density is used to describe the strength of a magnetic field. It is defined as the force acting on a current through a wire with the length l: Where is: B - magnetic flux density, F - force, I - current, l - length of the wire Therewith we get N/Am as the unit of the magnetic flux density. This unit is called Tesla, named after the Serb engineer Nikola Tesla, the unit symbol is T. In contrast to electric field lines, the magnetic field lines have no starting point or ending, but run in closed loops. There are no (macroscopic) magnetic monopoles, carrying "magnetic charge". Like the field lines of an electric field, they demonstrate direction and strength of a magnetic field. The field lines never cross each other. Permanent magnetsMagnetism can be observed at different materials. A non artificial magnetic material is Magnetite. This mineral consists out of iron(II,III) oxide with the chemical formula Fe3O4.Magnets produce a permanent magnetic field, being responsible for a force that attracts or repels other magnets. The field lines penetrate magnets, leaving at the north pole (usually marked red) and entering at the south pole (green). Insides the magnet the field lines run accordingly from the north to the south pole. The force between identical poles of two magnets repeals each other, different poles attract each other. For this reason, a magnet is tending to orient the magnetic moment parallel to the field when it is put inside an external magnetic field. The north pole is pointing towards the south pole of the external field. If the external field is inhomogeneous, the magnet is attracted by the area of higher field strength. 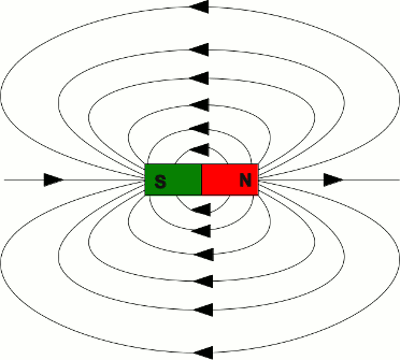
At the left picture you can see the field lines of a bar-shaped magnet. The field lines are running from the the red marked north pole to the green south pole. They don't stop at the south pole, but the lines inside the magnet (running from south to north) are not painted at the drawing. ElectromagnetismCharges moving with constant speed, generate a magnetic field. The according field lines are running in circles around the axis of movement. The direction of the field lines can be identified by using the "right hand grip rule": If the thumb of your right hand is pointing to the direction of the (positive) current and you grip the (imaginary) line of the current, your fingers are pointing to the direction of the magnetic field lines. Positive current means that positive charges are moving from the positive terminal to the negative terminal. The direction of the magnetic field lines stays the same, while negative charges are moving from the negative to the positive terminal instead.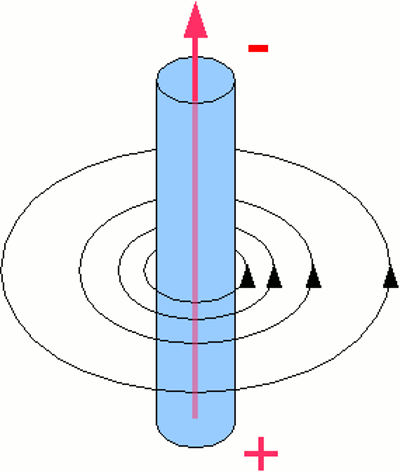
Magnetic field lines of an electric current. At the drawing, positive charges are moving from the positive to the negative terminal. The current is marked with a red arrow. The field lines are circles with the wire at their center. When looking from the top, the direction of the field lines is anticlockwise. In reality, negative charged electrons are moving from the positive to the negative terminal (bottom to top at the drawing), instead of positive charged atoms moving in the opposite direction. That doesn't have an influence on the direction of the magnetic field lines, because of the contrary charge and moving direction! Lorentz forceBecause of the fact that moving charges generate a magnetic field, they are influenced by an external magnetic field, too. This issue is used to quantify the "strength" of a magnetic field. As seen at the top of this page, the strength of the B-field is defined by the force acting on a current.This force is given by: Where is: B - magnetic flux density, F - force, q - charge, v - speed The resulting force is called Lorentz force, named after the Dutch physicist Hendrik Antoon Lorentz. The force is given by the vector cross product of speed and magnetic field. Both values are vectors, which makes the resulting force become a vector, too. The vector cross product is a binary operation on two vectors in a three dimensional Euclidian space, resulting in another vector being perpendicular on the plane containing the two input vectors. The three vectors generate a right-handed coordinate system, meaning they point to the direction of thumb, forefinger and middle finger of the right hand:
Where is: n - unit vector perpendicular to the plane containing v and B, Θ - angle between v and B Let's have a look at the case of v and B being perpendicular to each other, meaning the charges are moving perpendicular to the lines of the magnetic field. In this case sin Θ is 1 and the absolute value of the force becomes:
F = q * v * B For a wire with the length s in a perpendicular magnetic field, the Lorentz force can be calculated by the following substitutions: The definition of electric current is given by F = I * t * s/t * B = I * s * B Where is: F - Resulting Lorenz force, I - electric current, s - length of the wire, B - magnetic flux density That gives us the definition of the strength of a magnetic field, presented at the beginning of this page. Attention should be paid to the fact that wire and B-field have to be perpendicular to each other. Magnetic field strengthBesides the magnetic flux deinsity, the magnetic field strangth is used to describe magnetic fields. Both values are correlated by the following equation:
[3.17] Where is: H - Magnetic field strength, B - magnetic flux density, μ - magnetic permeability In SI-units, the magnetic field strength is measured in amperes per meter (A/m). <<< Resistance network Inductors >>> News The Project Technology RoboSpatium Contribute Subject index Archives Download Responses Games Links Gadgets Contact Imprint |
|
|