Hysteresekurve

Flussdichte gegen Feldstärke

Im vorangegangenen Kapitel haben wir die Vorgänge innerhalb eines ferromagnetischen Materials beim Anlegen eines äußeren Magnetfeldes kennen gelernt. Nun wollen wir uns das Ganze in Form eines Funktionsgraphen betrachten. Aufgetragen wird dabei die magnetische Flussdichte in Tesla auf der y-Achse gegen die magnetische Feldstärke in Ampere pro Meter auf der x-Achse. Die Feldstärke bezieht sich auf das von außen angelegte Magnetfeld, die Flussdichte auf die Magnetisierung des untersuchten Materials. Beide Variablen haben wir bereits im Kapitel Magnetismus kennen gelernt.

1.) Neukurve

Im vorherigen Kapitel habe wir bereits gesehen, dass die Stärke der Magnetisierung bei ferromagnetischen Stoffen von deren Vorgeschichte abhängt. Ein unmagnetisierter Nagel kann durch einen Permanentmagneten dauerhaft magnetisiert werden und besitzt anschließend ohne die Anwesenheit eines Magnetfeldes eine Restmagnetisierung. Wir wollen hier von einem zunächst unmagnetisierten Material ausgehen. Der Verlauf der Kurve beim erstmaligen Anlegen eines äußeren Magnetfeldes wird als Neukurve bezeichnet.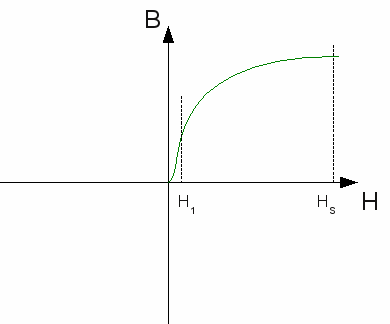

Neukurve eines ferromagnetischen Materials:
Zu Beginn des Versuchs liegt kein äußeres Magnetfeld an und das Material ist nicht magnetisiert, besitzt also kein nach außen gerichtetes Magnetfeld. Nun wird ein äußeres Magnetfeld angelegt und dessen Stärke allmählich gesteigert. Schon bei einer geringen Feldstärke beginnen sich die Spins (=Elementarmagnete) des Materials in Richtung des des äußeren Magnetfeldes auszurichten, womit die Flussdichte im Material immer stärker ansteigt. Dieser Anstieg wächst nicht ins Unendliche, sondern flacht im Punkt H₁ wieder ab. Es gibt halt nur eine begrenzte Anzahl Elementarmagnete (Atome) in einem Material und einige sind schwerer aus ihrer Ruhelage herauszudrehen als Andere. Das liegt im Wesentlichen an ihrer ursprünglichen Ausrichtung zum externen Magnetfeld und an der Gitterstruktur am Punkt des betreffenden Elementarmagneten. Die Java-Applikation hat gezeigt, dass Magnete die genau entgegengesetzt zum Magnetfeld ausgerichtet sind und dabei in der Gitterachse liegen, besonders schwer aus ihrer Ruhelage zu kippen sind und damit erst bei höheren Feldstärken umklappen. Je höher die Feldstärke des externen Magnetfeldes wird, um so mehr dieser "schwer zu drehenden" Magnete richten sich parallel zum Magnetfeld aus. Sobald sich alle Elementarmagnete in dem Material ausgerichtet haben. ist die Sättigungsmagnetisierung (H_S) erreicht.

2.) Langsames Abschalten des Magnetfeldes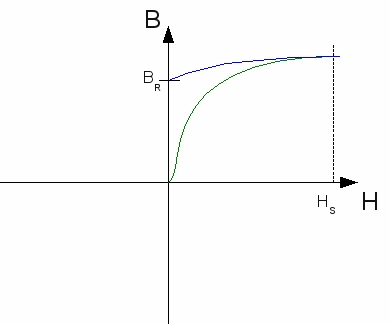

Die Feldstärke wird nun langsam auf Null reduziert. Einige der Elementarmagnete drehen sich dabei aus der Richtung des externen Magnetfeldes heraus. Das geschieht hauptsächlich bei solchen Atomen, deren Gitterachse in einem großen Winkel zur Richtung des Magnetfeldes stehen. Wie bereits im vorherigen Kapitel gesehen, bleiben jedoch (abhängig vom Material) einige Elementarmagnete in Richtung zum ursprünglichen Magnetfeld stehen (oder zumindest in einem kleinen Winkel dazu). Nach Abschalten des Magnetfeldes bleit das Material also teilweise magnetisiert. Diese Restmagnetisierung wird Remanenz (B_R) genannt.

3.) Anlegen eines gegengerichteten Magnetfeldes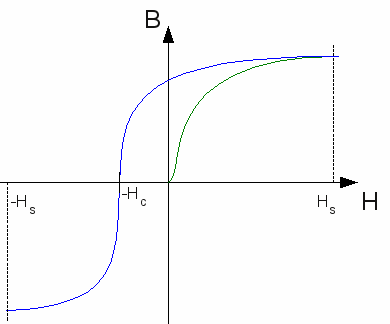

Nun legen wir ein Magnetfeld an, dessen Feldlinien um 180 Grad gegenüber dem ursprünglichen Feld gedreht sind. Wo sich zuvor der magnetische Nordpol befand, ist nun der Südpol. Wir bewegen uns in unserem Koordinatensystem also auf der x-Achse nach links.
Wiederum beginnen sich die Elementarmagnete in Richtung des externen Magnetfeldes zu drehen. Der Startpunkt der magnetischen Flussdichte liegt nun aber nicht im Koordinatenursprung. Das Material besitzt ja nach wie vor eine Restmagnetisierung, verursacht durch das ursprüngliche Magnetfeld. Bei einem bestimmten Wert für die Feldstärke sinkt die Flussdichte in dem Material auf Null. Nun sind die Elementarmagnete in ihren Richtungen so verteilt, dass das Material wieder entmagnetisiert ist. Die Feldstärke, die zum Entmagnetisieren benötigt wird, nennt man Koerzitivfeldstärke (-H_C). In diesem Punkt schneidet die Kurve die x-Achse.
Wird die Feldstärke des gegenpoligen Magnetfeldes weiter erhöht, d.h. wir bewegen uns auf der x-Achse weiter nach links, wird auch hier irgendwann der Punkt erreicht, an dem alle Elementarmagnete parallel zum externen Feld ausgerichtet sind. Die Sättigungsmagnetisierung ist erneut erreicht, jedoch sind alle Elementarmagnete um 180 Grad gedreht. Ausgedrückt wird das durch ein negatives Vorzeichen (-H_S).

4.) Abschalten des gegengerichteten Magnetfeldes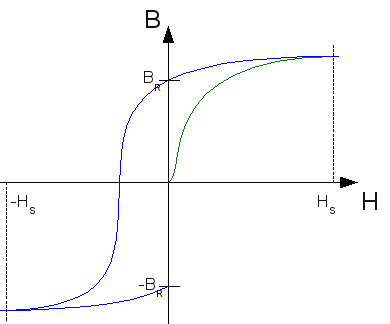

Nun reduzieren wir wieder die Feldstärke des externen Magnetfeldes auf Null. Dabei drehen sich wieder einige Elementarmagnete aus ihrer momentanen Lage heraus, wobei die Flussdichte in dem Material sinkt. Hier sind wiederum die Elementarmagnete (Atome) betroffen, deren Gitterachse in einem großen Winkel zu den Feldlinien des externen Magnetfeldes stehen. Da das gegengerichtete Feld um 180 Grad gegenüber dem ursprünglichen Magnetfeld gedreht war, ist der Winkel wiederum groß zur Gitterachse der selben Atome, die sich beim Abschalten des ursprünglichen Magnetfeldes als erstes herausgedreht haben. Nach dem Abschalten des externen Gegenfeldes bleiben also in der Regel die selben Elementarmagnete stehen, die das auch beim ursprünglichen Feld gemacht haben, nur mit dem Unterschied, dass diese ebenfalls um 180Grad verdreht sind! Die Folge davon ist, das die Restmagnetisierung gleich groß wie beim ursprünglichen Feld ist, jedoch mit negativem Vorzeichen. Wo zuvor der Nordpol des magnetisierten Eisenstücks war, ist nun der Südpol und umgekehrt.

5.) Erneutes Anlegen eines Magnetfeldes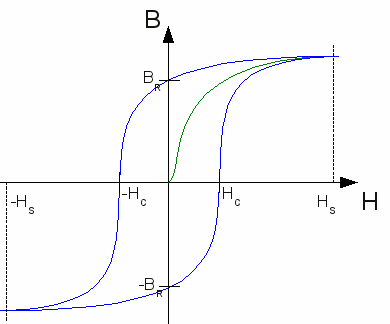

Legen wir nun wieder ein externes Magnetfeld mit der ursprünglichen Richtung an, laufen wieder die Prozesse analog zur Neukurve ab, mit dem Unterschied, dass wir nicht im Koordinatenursprung starten, da das Werkstück noch die Restmagnetisierung (-B_R) des Gegenfeldes besitzt. Erst im Punkt H_C, dem erneuten Schnittpunkt mit der x-Achse ist das Material entmagnetisiert. Zum Erreichen dieses Zustandes ist jedoch das Vorhandensein einer von Null verschiedenen Feldstärke - der Koerzitivfeldstärke - notwendig.
Der Wert für die Sättigungsmagnetisierung ist gleich groß dem Wert für die Neukurve und somit schließt sich hier die Schleife. Schalten wir das Magnetfeld erneut ab, erhalten wir wieder genau den Kurvenverlauf wie unter Punkt 2.) beschrieben.

<<< Magnetische Hysterese Ferromagnetismus >>>

Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum