Elektromagnetische Induktion

Umkehrprinzip

Im Kapitel Magnetismus haben wir gelernt, dass eine sich bewegende Ladung ein Magnetfeld verursacht. Wie man Ladungen bewegen kann, haben wir noch weiter vorne in den Kapiteln zu Spannung und Strom gesehen. Bündeln kann man Magnetfelder, indem man den Draht in Form einer Spule anordnet. Somit kann man ein Magnetfeld erzeugen, indem man eine Spannung an die Drahtenden einer Spule anlegt. Ist der umgekehrte Vorgang, also das Generieren einer Spannung durch ein Magnetfeld in einer Spule, ebenfalls durchführbar? Fast alle physikalischen Gesetze sind derart umkehrbar. Als Beispiel nenne ich einmal das wassergetriebene Mühlrad: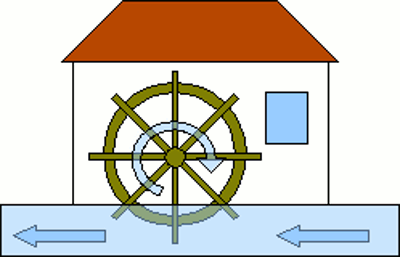

Abbildung 1:
Strömt das Wasser wie in diesem Bild gezeigt, von rechts nach links an dem Mühlrad vorbei, so wird dadurch selbiges im Uhrzeigersinn in Rotation versetzt.
Die Frage lautet nun: "Was passiert, wenn man das Mühlrad mit Hilfe eines Motors entgegen dem Uhrzeigersinn dreht?"
Nun, dann wirkt das Mühlrad wie eine Pumpe und treibt das Wasser nach rechts.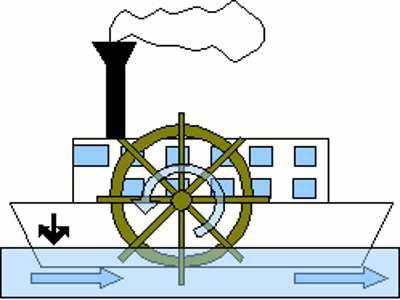

Abbildung 2:
Dass eine Mühle einen Fluss bergauf pumpt, habt ihr bestimmt noch nicht gesehen, aber eine andere Anwendung dieses Prinzips dürfte euch aus Filmen der "Guten, alten Zeit" durchaus bekannt sein: Der Schaufelraddampfer.

Induktionsgesetz

Das Problem, Spannung mit Hilfe einer Spule und einem Magneten zu erzeugen, beschäftigte unter Anderem den englischen Experimentalphysiker Michael Faraday. Er gilt als der Entdecker des Prinzips der elektromagnetischen Induktion. Herausgefunden hat er den folgenden Zusammenhang:

Die in einem geschlossenen elektrischen Leiter erzeugte elektromotorische Kraft ist proportional zur Änderung des magnetischen Flusses durch die von der Leiterschleife gebildete Oberfläche.

Mathematisch ausgedrückt lautet die Formel:

[3.23]

Dabei bedeutet:
ε - Elektromotorische Kraft in Volt, Φ_B - Magnetischer Fluss in Weber

Die elektromotorische Kraft haben wir bereits als Differenz zweier Potentiale in einem elektrischen Feld kennen gelernt. Die üblichere Bezeichnung lautet "Spannung".
Den magnetischen Fluss haben wir noch nicht direkt erwähnt, wir kennen aber bereits den Begriff der magnetischen Flussdichte. Bildlich gesprochen entspricht die magnetische Flussdichte der Anzahl der magnetischen Feldlinien durch eine dazu senkrecht stehende Fläche. Der magnetische Fluss entspricht dabei der "Netto-Summe" der Feldlinien durch eine beliebig orientierte Fläche. Da Feldlinien einer Richtung folgen, ist die Netto-Summe die Anzahl der Feldlinien in einer Richtung minus der Anzahl entgegengesetzt verlaufender Feldlinien. Etwas genauer gesagt, wird die Flussdichte an jedem Punkt der beliebig gekrümmten Fläche aufsummiert, womit auch hier nur der senkrecht verlaufende Feldanteil berücksichtigt wird.

Praktische Bedeutung

Um eine Spannung zu erzeugen, müssen wir also den magnetischen Fluss durch einen zur Schleife verbundenen elektrischen Leiter ändern. Unpraktischerweise lässt sich die generiere Spannung in einer geschlossenen Leiterbahn nur schlecht messen. Unterbrechen wir also die Schleife an einer kleinen Stelle und messen an den Endpunkten die auftretende Spannung. Ein weiteres Prinzip vereinfacht die Messung: Nehmen wir statt nur einer Schleife gleich mehrere Schleifen, in denen der magnetische Fluss gleichermaßen geändert wird, so ist die Gesamtspannung gleich der Summe der Einzelspannungen. Eine Anordnung bestehend aus vielen Leiterschleifen haben wir bereits als Spule kennen gelernt. Für Spulen gilt also:

[3.24]

Dabei bedeutet:
N - Anzahl der Spulenwicklungen ε - Elektromotorische Kraft in Volt, Φ_B - Magnetischer Fluss in Weber

Nun müssen wir also nur noch den magnetischen Fluss durch die Leiterschleifen variieren, um eine elektrische Spannung zu generieren. Nehmen wir dazu einen Permanentmagneten und eine Spule mit drei Windungen: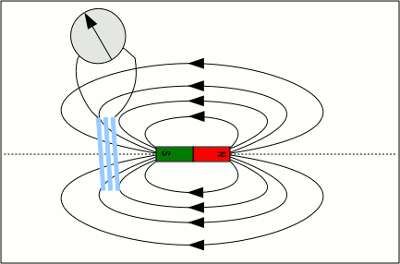

Abbildung 3: Animation startern
Eine Spule mit 3 Windungen, deren Enden an ein Spannungsmessgerät angeschlossen sind, wird über einen stabförmigen Permanentmagneten gezogen. Die magnetischen Pole liegen bei diesem Vorgang auf der Achse der Spule. Wird die Spule mit konstanter Geschwindigkeit an den magnetischen Nordpol herangeführt, so nimmt die Anzahl der durch die Spule verlaufenden Feldlinien und damit auch die Flussdichte zu. Dem Induktionsgesetz zu Folge wird damit eine Spannung induziert, der Zeiger des Messgerätes schlägt nach rechts aus. Trotz konstanter Bewegungsgeschwindigkeit steigt die induzierte Spannung an, je näher die Spule an den magnetischen Nordpol herankommt. Das hängt damit zusammen, dass die Feldlinien an den magnetischen Polen dichter verlaufen, der Betrag der Flussdichte steigt zu den Polen hin überproportional an. Kurz bevor die Spule den Magneten erreicht, ist die höchste Spannung zu verzeichnen. Sobald der Magnet in die Spule eintaucht, verlaufen alle Feldlinien durch die Schleifen der Spule (innerhalb des Magneten). Die Flussdichte steigt nicht weiter an und damit fällt die induzierte Spannung auf Null. So lange nun beide Pole aus der Spule herausragen, ändert sich der magnetische Fluss durch die Spule nicht mehr. Erst wenn die Spule den Magneten an dessen Südpol verlässt, sinkt die Anzahl der durch sie verlaufenden Feldlinien wieder - zunächst stärker, da die Feldlinien um den Südpol gebündelt verlaufen, dann zunehmend langsamer, da die Flussdichte mit zunehmendem Abstand vom Südpol überproportional geringer wird. Der Zeiger des Spannungsmessers schlägt in die Gegenrichtung aus - erst stark, mit zunehmender Entfernung immer geringer.
Die durch einen sich zeitlich ändernden magnetischen Fluss hervorgerufene Spannung nennt man Induktionsspannung.

<<< Ferromagnetismus Wirbelstrom >>>

Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum