|
|
|
|
News The Project Technology RoboSpatium Contribute Subject index Download Responses Games Gadgets Contact <<< Torque curve Model motor >>> Power outputTorque and PowerAs per definition, Power is the performed work per time interval. The work done by a constant force of a given magnitude on a point that moves a displacement in the direction of the force is the product force times displacemant. At the previous chapter, the torque of a motor was treated. Knowing the magnitude of torque and the length of the lever (diameter of the wheel attached to the motor) we can calculate the work performed by a motor with each revolution: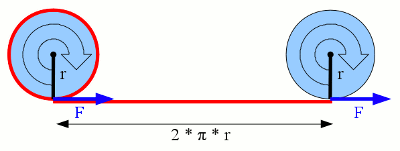
Work performed by a motor with a given torque. With a given torque we can calculate the force acting on the outer diameter of a wheel with radius r attached to the motor. While rolling to the right by one revolution as drawn at the picture, the distance covered is With Where is: W - performed work respectively converted energy, M - torque of the motor The rotational speed respectively speed of revolution is: Where is: n - rotational speed, ΔN - number of revolutions, Δt - time interval The Si-unit is 1/s or s-1. Another common unit is revolutions per minute 1/min or min-1. With the rotational speed the power output is: Where is: P - power, t - time, W - performed work respectively converted energy, M - torque of the motor, n - rotational speed of the motor Power and efficiencyWith constant torque the correlation between rotational speed and output power of a motor is linear: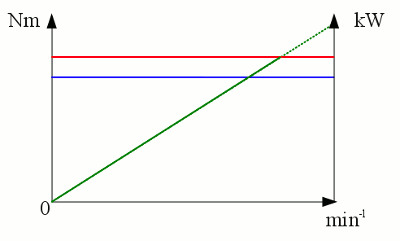
Torque (blue), output power (green) and input power (red) of an electric motor with a constant torque. As per definition efficiency is the useful (mechanical) work per quantity of (electrical) input energy which is equivalent to the mechnical output power per input power. At the point of origin the efficiency is zero (constant input power but no movement, thus no output power). Moving slightly to the right of the X axis at the drawing above, the output power is increasing by what the efficiency becomes (slightly) different from zero, being is still bad. Moving some more units to the right, the output power and for this reason the efficiency is increasing constantly. At the point of intersection between the green and the red line the output power equals the input power hence the efficiency is 1 (100%). Moving to the right of that point, the output power overruns the input power! Who ever can built an electric motor like that will turn physical laws upside down! The theoretically highest value for efficiency is 100%, something that can't be reached in praxis. As we will see some later the input power has to be raised to keep the torque high at high revolution speeds. Vice versa the torque is decreasing with increasing revolution sped if the input power is kept constant: 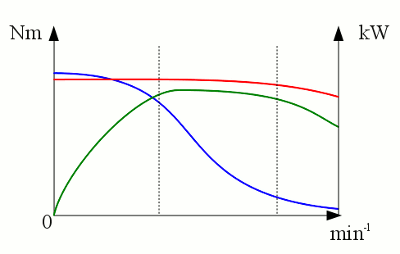
Torque (blue), output power (green) and input power (red) of an electric motor with non constant torque. Based on the torque curve of the previous chapter the output power is increasing to a maximum and falling below that peak with increasing revolution speed. The (mechanical) output power is always lower than the (electric) input power, by what the efficiency is lower than 100% at all given points. The efficiency is high inside the marked area with an output power being just slightly lower than the input power. <<< Torque curve Model motor >>> News The Project Technology RoboSpatium Contribute Subject index Archives Download Responses Games Links Gadgets Contact Imprint |
|
|