|
|
|
|
Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Download Reaktionen Spiele Gadgets Kontakt <<< Spannung Strom, Widerstand und Leistung >>> KondensatorArbeit im elektrischen FeldIm vorherigen Kapitel haben wir gesehen, dass Arbeit an Ladungen im elektrischen Feld verrichtet wird, wenn diese entgegen der gerichteten Kraftwirkung in dem Feld bewegt werden. Ferner haben wir gelernt, dass die zum Verrichten der Arbeit pro Ladung nötige Energie einen sehr verbreiteten Namen trägt, nämlich "elektrische Spannung".Metalle sind Materialien in denen sich bewegliche Ladungen befinden. Anlegen einer Spannung an den Enden eines leitenden Drahtes bedeutet nichts anderes, als den Draht längs seiner Ausrichtung einem elektrischen Feld auszusetzen. Die in dem Draht befindlichen Ladungen werden folglich verschoben. 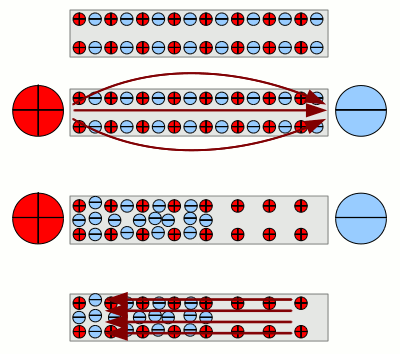
Modell eines elektrisch leitenden Drahtes im Querschnitt. Im Inneren befinden sich bewegliche, negativ geladene Elektronen (blau mit Minuszeichen) und positiv geladene, ortsfeste Atomrümpfe (rot mit Pluszeichen). Befindet sich der Draht im feldfreien Raum, so sind die negativ geladenen Elektronen und die positiv geladenen Atomrümpfe gleichmäßig über das Volumen des Drahtes verteilt. Das Anlegen einer Spannung an den Enden des Drahtes ist gleichzusetzen mit dem Anlegen eines äußeren elektrischen Feldes (dunkelrote Feldlinien). Dargestellt wird das durch eine positive bzw. negative Ladung außerhalb des Drahtes an dessen Enden. Durch das äußere Feld wirkt eine Kraft auf die Ladungen im Draht. Die positiv geladenen Atomrümpfe sind unbeweglich und verbleiben damit in ihrer Position. Anders ist die Situation bei den beweglichen Elektronen. Diese bewegen sich der Kraftwirkung folgend nach links, hin zur positiven Ladung des äußeren Feldes. Dadurch kommt es zu einer ungleichmäßigen Verteilung der Ladungen innerhalb des Drahtes. Ungleichmäßig verteilte Ladungen wiederum erzeugen ein elektrisches Feld. Die Elektronen verteilen sich derart, dass das elektrische Feld im Innern des Drahtes gleich stark, aber entgegengesetzt zum äußeren Feld ist. Sobald dieser Zustand erreicht ist, stoppt die Bewegung der Elektronen und die beiden Felder heben sich im Inneren des Drahtes auf. Entfernen wir nun die äußeren Ladungen - sprich wir reduzieren die Spannung auf Null - bleibt nur das innere elektrische Feld der ungleichmäßig verteilten Elektronen und Atomrümpfe zurück. Dieses ist entgegengesetzt zu dem ursprünglich vorhandenen äußeren Feld gerichtet. In diesem Feld tritt wiederum eine Kraftwirkung auf die Ladungen auf, die bewirkt, dass sich die Elektronen wieder gleichmäßig über den Draht verteilen. Ladungstrennung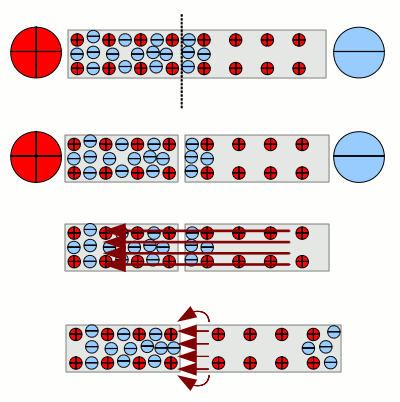
Trennen wir nun den Draht an der markierten Stelle, während die äußere Spannung noch vorhanden ist und schieben die beiden Teilstücke ein wenig auseinander. Was passiert, wenn wir jetzt die Spannung auf Null reduzieren? Es verbleibt wie im ersten Fall nur das elektrische Feld im Innern des Drahtes. Erneut bewegen sich die Elektronen der durch dieses Feld hervorgerufenen Kraftwirkung folgend. An der Schnittstelle können die Elektronen jedoch nicht mehr in den rechten Teil des Drahtes gelangen. Es verbleibt also zwangsläufig ein Überschuss an Elektronen in der linken Drahthälfte und ein Überschuss an positiv geladenen Atomrümpfen in der rechten Drahthälfte. Als Folge dieser verbleibenden Ungleichverteilung der Ladungsträger baut sich das innere Feld in dem Draht nicht vollständig ab. Es ist jetzt sogar messbar in dem Außenbereich an der Schnittstelle. Die auf die Elektronen und Protonen wirkende Kraft überträgt sich auf die beiden Drahtstücke. Zwischen diesen wirkt jetzt eine messbare Kraft. Die beiden Teilstücke verhalten sich wie zwei große Ladungsträger. 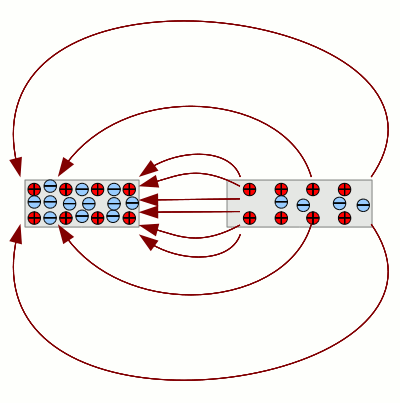
Das wird um so deutlicher, je weiter die beiden Teilstücke voneinander getrennt werden. Der zunehmende Abstand zwischen den Drahtstücken bewirkt - ähnlich dem Coulomb-Gesetz - eine geringer werdende Wechselwirkung. Innerhalb der Teilstücke verteilen sich die Elektronen zunehmend gleichmäßig. Leitende Verbindung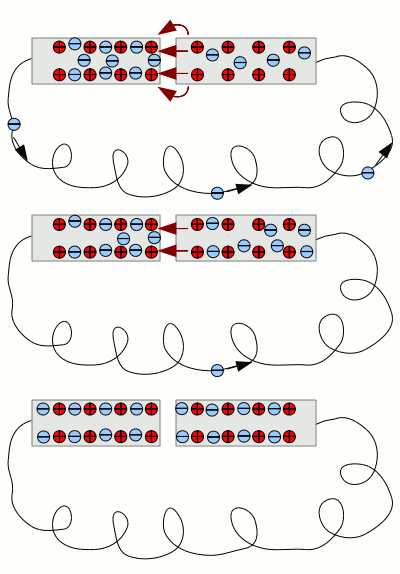
Nun verbinden wir die beiden Drahtstücke wieder elektrisch leitend. Das muss nicht zwingend geschehen, indem wir die beiden Teile an ihrer Schnittstelle wieder zusammenfügen. Wir nehmen also einen weiteren dünnen Draht und führen die Verbindung "von hinten" aus. Auf die Elektronen wirkt in dem elektrischen Feld nicht nur eine Kraft direkt zwischen den beiden Drahtstücken, sondern auch entlang anderer Feldlinien, die mitunter "hintenrum" führen. Es bewegen sich daher die überschüssigen Elektronen von dem linken Drahtstück über die dünne Verbindung zu dem rechten Drahtstück. Das elektrische Feld zwischen den beiden Drahtstücken wird zunehmend schwächer. Im Endzustand sind in beiden Drahtstücken wieder genau so viele Elektronen wie Atomrümpfe und die Elektronen sind gleichmäßig über die beiden Drahtstücke verteilt. EnergiebetrachtungBei der Verschiebung von Ladungen (Elektronen) in einem elektrischen Feld wird Arbeit verrichtet oder Energie freigesetzt. Zunächst haben wir die Ladungen durch Anlegen einer äußeren Spannung voneinander getrennt. Das Anlegen der Spannung hat Energie von außen in das System eingebracht. Diese Energie hat zur Ungleichverteilung der Elektronen in dem Drahtstück geführt. Das Durchtrennen des Drahtes in zwei Teile hat die Energie des Systems nicht beeinflusst. Nun haben wir die Spannung auf Null gesenkt. Dazu mussten wir ebenfalls Energie aufwenden! Das Abschalten der äußeren Spannung entspricht nämlich dem "Wegziehen" der äußeren Ladungen entgegen der anziehenden Wirkung der beiden Drahtstücke! Nun haben wir die beiden Drahtstücke auseinander gezogen. Auch dabei wird mechanische Arbeit entgegen dem elektrischen Feld zwischen den beiden Stücken verrichtet. Wir können nämlich die beiden Drahtstücke als unterschiedlich geladene Partikel betrachten und um diese voneinander zu trennen muss Arbeit verrichtet werden.Nun haben wir die beiden Stücke wieder elektrisch leitend verbunden. Jetzt konnten sich die Elektronen wieder der Kraftwirkung in dem elektrischen Feld folgend gleichmäßig verteilen. Dieser letzte Prozess lief freiwillig ab, es wurde dabei die zuvor aufgewendete Energie wieder freigesetzt. KondensatorEin Kondensator ist ein elektrisches Bauelement, das elektrische Ladung und damit Energie speichern kann. Kondensatoren bestehen zumeist aus zwei dicht beieinander liegenden Platten aus elektrisch leitendem Material, die durch einen Isolator voneinander getrennt sind. Wie bei dem oben genannten Beispiel mit dem durchtrennten Draht kann mit dieser Anordnung Ladung getrennt voneinander "aufbewahrt" werden. Die Ladungstrennung wird dabei durch das Verbinden mit einer Spannungsquelle vorgenommen. In dem oberen Beispiel haben wir die externe Spannung durch das "heranbringen" von externen elektrischen Ladungen erzeugt. In elektrischen Schaltkreisen verwendet man hingegen "Elektronenpumpen". Derartige Spannungsquellen werden elektrisch leitend mit dem Stromkreis verbunden und erzeugen eine Spannung in dem Stromkreis, indem sie Elektronen auf der einen Seite (=Minuspol) in den Kreis pumpen und diese auf der anderen Seite (=Pluspol) absaugen. Dabei werden so lange Elektronen gepumpt bzw. abgesaugt, bis die entsprechende Spannung der Spannungsquelle erreicht ist. Wird ein Kondensator mit einer derartigen Spannungsquelle verbunden, werden in die eine Platte Elektronen gepumpt und auf der anderen Seite abgesaugt. Das geschieht so lange, bis das sich zwischen den Platten aufbauende elektrische Feld ein vom Betrag her gleich großes, aber entgegengerichtetes Potential aufgebaut hat (ähnlich dem Beispiel oben).Trennen wir nun den Kondensator von der Spannungsquelle, so kann man an dessen Klemmen nach wie vor die von der Spannungsquelle bereitgestellte Spannung messen. erst wenn die beiden Klemmen verbunden (kurzgeschlossen) werden, fließen die Elektronen von der linken zur rechten Kondensatorplatten und die Spannung sinkt auf Null. 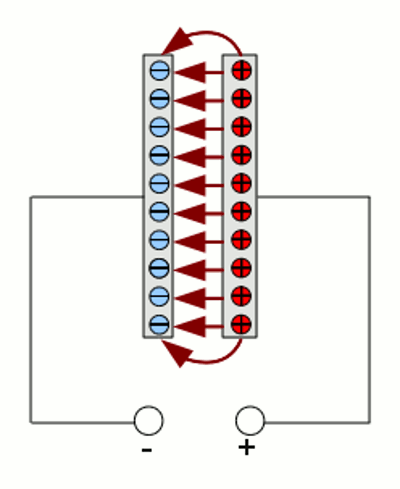
Schematische Darstellung eines Kondensators: Die Spannungsquelle pumpt Elektronen in die linke Platte und saugt diese auf der rechten Seite ab. Damit verbleiben auf der rechten Seite überschüssige Positive Ladungen (Atomrümpfe). Zwischen den Platten baut sich entsprechend ein elektrisches Feld auf, dessen Potentialdifferenz der angelegten Spannung entspricht und diesem entgegengesetzt ausgerichtet ist. Je kleiner der Abstand zwischen den beiden Platten und je größer die Ausdehnung, um so mehr Elektronen müssen in die Platten gepumpt bzw. abgesaugt werden, bis diese Gegenspannung erreicht ist. Auch das zwischen den Materialien befindliche Material übt Einfluss auf das elektrische Feld zwischen den Platten und damit die Anzahl der zu pumpenden Elektronen aus. Für die Ladungsmenge in einem Kondensator erhalten wir: Dabei bedeutet: U - Spannung, C - Kapazität, Q - Ladung Und für die gespeicherte Energie: Dabei bedeutet: W - Energie, U - Spannung, C - Kapazität Der Faktor C gibt die Kapazität des Kondensators an. Diese Kapazität ist ein durch die Bauform gegebener fester Wert. Darin geht die Plattengröße, der Abstand zwischen den Platten und die Materialeigenschaft des Isolatormaterials zwischen den Platten ein. Die Kapazität eines Kondensators wird in Farad angegeben. Die Einheit wurde nach dem englischen Experimentalphysiker Michael Faraday benannt und wird mit dem Buchstaben F abgekürzt. Die Ladungsmenge auf einem Kondensator steigt also proportional zur angelegten Spannung und die gespeicherte Energiemenge proportional zum Quadrat der angelegten Spannung. <<< Spannung Strom, Widerstand und Leistung >>> Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum |
|
|