|
|
|
|
Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Download Reaktionen Spiele Gadgets Kontakt <<< Drehmoment Leistungsbilanzen >>> FahrzeugauslegungEnergieumwandlung beim BeschleunigenEin Fahrzeug wird beschleunigt, wenn eine Kraft auf dieses einwirkt. Im Kapitel über die Beschleunigung sind wir von einer konstanten Kraftwirkung während des gesamten Beschleunigungsvorganges ausgegangen. Aus Formel [2.12] ist ersichtlich, dass die Energie quadratisch mit der Geschwindigkeit anwächst. Beschleunigt ein Fahrzeug konstant, d.h. dass der Geschwindigkeitszuwachs pro Zeiteinheit konstant ist, so steigt die verrichtete Arbeit pro Zeiteinheit (=Leistung) ebenfalls quadratisch an. Dummerweise haben wir keine unbegrenzte Leistung zur Verfügung, sondern lediglich eine von der Antriebseinheit abhängige Maximalleistung. Ausgedrückt in Formeln ergibt sich für Beschleunigungsvorgänge:
P = Leistung, m - Fahrzeugmasse, v - Geschwindigkeit, t - Zeit Gehen wir von den Eckdaten des Projektfahrzeuges vor den Umrüstung aus, so ergibt sich mit dem originalen Verbrennungsmotor eine Leistung von 17kW bei einem Fahrzeuggewicht von 765kg (bei halber Zuladung). Ausgehend von Formel [2.15b] ergibt sich somit für die Beschleunigung von 0 auf 100km/h (0 auf 27,8m/s) eine Zeit von t = 17,4s. Reale Messwerte ergeben jedoch mehr als 30 Sekunden für den Sprint auf 100km/h. Das liegt daran, dass ein Verbrennungsmotor nicht bei jeder Drehzahl seine Maximalleistung abgibt. Im Mittel steht für den Beschleunigungsvorgang somit nur eine geringere Leistung zur Verfügung. Berechnen wir umgekehrt die mittlere Leistung während eines Beschleunigungsvorganges von 0 auf 100km/h innerhalb von 35s, so ergibt sich mit Hilfe von Formel [2.15a] eine Leistung von gerade einmal P = 8,4kW. Die Wahrheit liegt irgendwo dazwischen, denn wir haben bislang die Verluste durch Luftwiderstand und Rollreibung außer acht gelassen. LuftwiderstandIm Gegensatz zu Beschleunigungsvorgängen ändert sich beim Dahinfahren mit konstanter Geschwindigkeit die mechanische Energie des Fahrzeugs nicht. In der realen Welt muss zum Aufrechterhalten der Geschwindigkeit dennoch beständig Energie aufgewendet werden. Ursache dafür ist der Luft- und Rollwiderstand. Aus Formel [2.9] im Kapitel zum Luftwiderstand ergibt sich die zu überwindende Kraft in Abhängigkeit zur Fahrzeuggeschwindigkeit. Im Kapitel zu Arbeit, Energie und Leistung haben wir ferner gelernt, dass die Energie gleich der Kraft multipliziert mit der zurückgelegten Wegstrecke ist. Damit ergibt sich:
P - Leistung, ρ - Dichte der Luft, CW - Luftwiderstandsbeiwert, A - Stirnfläche des Fahrzeugs, v - Geschwindigkeit, t - Zeit, s - Wegstrecke, E - Energie Aus Formel [2.16] ergibt sich, dass die benötigte Leistung zur Überwindung des Luftwiderstandes mit der dritten Potenz zur Fahrzeuggeschwindigkeit steigt. Damit wird schnell klar, dass sich hohe Reichweite und hohe Fahrzeuggeschwindigkeit nur schlecht vereinbaren lassen. Mit den Daten für das Projektfahrzeug (CW=0,47 A=1,51m2) ergeben sich bei einer Luftdichte von 1,2041 kg/m3 folgende Werte:
Mehr als 9kW (13PS) nur um den Luftwiderstand bei einer Geschwindigkeit von 100km/h zu überwinden, ist schon eine Menge Leistung für ein Elektrofahrzeug mit begrenzten Energiereserven an Bord. Noch mehr Leistung wird benötigt, wenn es bergauf geht. Steigungen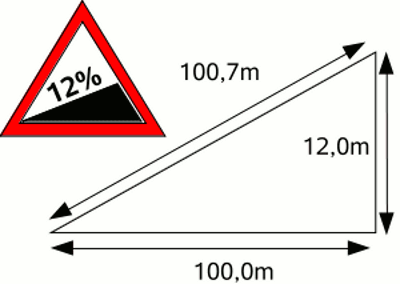
Wie in Formel [2.11] zu sehen, wird auch beim Anheben von Massen Arbeit verrichtet. Entsprechend wird Leistung benötigt, um mit einem Auto mit konstanter Geschwindigkeit bergauf zu fahren. Steigungen werden im Straßenverkehr in Prozentwerten angegeben. Dabei wird angegeben um welche Höhendifferenz eine Straße auf 100m steigt. 12% Steigung bedeutet, dass die Straße auf 100m in waagerechter Richtung um 12m ansteigt. Zu beachten ist dabei, dass die Fahrstrecke zur Überwindung von 12m Höhendifferenz etwas länger ist (in diesem Fall 100,7m). Umgekehrt errechnet sich die überwundene Höhendifferenz pro 100m Fahrstrecke zu: Δhist = 100 * Δhgeg / √(1002 + Δhgeg2) Dabei bedeutet: Δhist - Höhendifferenz pro 100m Fahrstrecke, Δhgeg - Höhendifferenz pro 100m waagerechter Strecke Es gilt:
EPot - Potentielle Energie, m - Masse, g - Gravitationsbeschleunigung, h - Höhendifferenz, P - Leistung, t - Zeit, x - Höhendifferenz pro 100m Fahrstrecke in Prozent, s - Fahrstrecke, v - Geschwindigkeit
Reichlich viel Leistung die abgezweigt wird, um Steigungen zu erklimmen. Von unschätzbarem Vorteil ist hingegen, dass diese Leistung unserem Fahrzeug unentgeltlich wieder zur Verfügung gestellt wird, wenn man Gefällstrecken fährt. Energie zur Überwindung von Roll- und Luftwiderstand gehen unweigerlich verloren. Rollwiderstand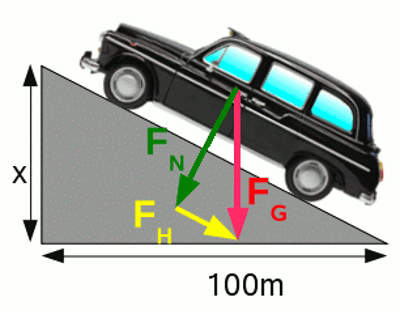
Der kleinste "Leistungsvernichter" ist der zu überwindende Rollwiderstand. Die dabei bremsende Kraft ist - wie aus Formel [2.5] ersichtlich - von der Fahrzeuggeschwindigkeit unabhängig. Lediglich die Normalkraft, also der Kraftanteil welcher das Fahrzeug auf den Boden presst, geht in die Rechnung ein. Auf ebener Strecke ist das die Gewichtskraft des Fahrzeugs. An Steigungen teilt sich die Gewichtskraft in die Komponenten Hangabtriebskraft und Normalkraft auf. Für den Zusammenhang zwischen Steigung und Normalkraft gilt: FH / FN = x / 100 Daraus ergibt sich: FH = x * FN / 100 Nach dem Satz von Pythagoras gilt: FH2 + FN2 = FG2 und man erhält: FN = √(FG2 / (x2 / 10000 + 1)) Bei korrektem Luftdruck ist der Rollwiderstandskoeffizient von Autoreifen auf Asphalt circa 0,012. Auf gerader Strecke, also bei maximaler Normalkraft ergibt sich daraus eine abbremsende Kraft von: FR = 0,012 * 765kg * 9,81m/s2 = 90,0558N (Bei 15% Steigung reduziert sich FR auf 89.0595N) Für den Leistungsverlust erhalten wir: ER = FR * s = P * t oder P = FR * s / t = FR * v dabei gilt: FR - Rollreibungskraft, s - Strecke, t - Zeit, v - Geschwindigkeit, ER - Energieverlust durch Rollreibung, P - Leistung
<<< Drehmoment Leistungsbilanzen >>> Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum |
|
|