|
|
|
|
Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Download Reaktionen Spiele Gadgets Kontakt <<< Schaltvorgänge Schwingkreise >>> Energie von MagnetfeldernElektrische EnergieIn Formel [3.8] haben wir die elektrische Leistung als das Produkt aus Spannung und Stromstärke kennen gelernt. Analog zur mechanischen Arbeit ist auch die elektrische Arbeit gleich dem Produkt aus Leistung und Zeit:Dabei bedeutet: Wel - elektrische Arbeit, Pel - elektrische Leistung, U - Spannung, I - Strom, t - Zeit In ohmschen Widerständen wird elektrische Energie in Wärmeenergie umgewandelt. Gleichung [3.38] zeigt, dass die dabei "verbratene" Energiemenge bei konstanter Spannung (und damit konstantem Strom), proportional zur Zeit ist. Um ein Magnetfeld in einer Spule aufzubauen, muss elektrische Energie aufgewendet werden. Betrachten wir eine Spule ohne ohmschen Widerstand: Bei konstanter Eingangsspannung ist der durch diese fließende Strom keinesfalls konstant. Aus der Beziehung:
Wel - elektrische Arbeit bzw. Energie, Pel - elektrische Leistung, I - Strom, U - Spannung, L - Induktivität, t - Zeit Energie verschwindet nicht irgendwo im Nirwana, sondern wird stets von einer in eine andere Form umgewandelt. Im Kondensator geschieht das durch den Aufbau eines elektrischen Feldes, in dem die geladenen Teilchen potentielle Energie besitzen. In ohmschen Widerständen wird die elektrische Energie in Wärmeenergie gewandelt (=kinetische Energie der Atome). Was passiert mit der elektrischen Energie die wir in die Spule gesteckt haben? Nun diese Energie steckt vollständig in dem Magnetfeld, das die Spule erzeugt hat, da wir von einer idealen Spule ohne ohmschen Widerstand ausgegangen sind. Diese Vorstellung ist aus der Praxis heraus schwierig nachzuvollziehen, da hier immer verlustbehaftete Spulen zum Einsatz kommen. Nehmen wir einen Kondensator und schließen diesen an eine Batterie an, so fließt ein Strom, bis der Kondensator aufgeladen ist. Nun können wir den Kondensator abklemmen die in diesem gespeicherte Energie bleibt erhalten. Auch Stunden später können wir die Spannung an dem Kondensator messen und die gespeicherte Energie jederzeit entnehmen, indem wir z.B. einen elektrischen Verbraucher (Motor, Lampe usw.) an dem Kondensator anschließen. Nehmen wir nun eine Spule und schießen diese an die Batterie an, so baut sich ein Magnetfeld auf, in dem ebenfalls Energie steckt. Die Spule können wir nun aber nicht einfach abklemmen, um das Magnetfeld zu erhalten und die Energie zu speichern! Das Magnetfeld bleibt ja nur dann konstant, wenn der durch die Spule fließende Strom ebenfalls konstant bleibt (Siehe Kapitel Induktion und Selbstinduktion). Wir müssten also gleichzeitig mit dem Wegnehmen der Batterie die Enden der Spule kurzschließen. Das ist so einfach nicht machbar und selbst wenn uns das gelänge, würde die in der Spule bzw. dem Magnetfeld gespeicherte Energie nicht über Stunden hinweg erhalten bleiben. Der Strom im Spulendraht fließt ja weiter und wird aufgrund des ohmschen Widerstandes nach und nach in Wärmeenergie umgewandelt. Es läuft der in Formel [3.36] und [3.37] beschriebene verlustbehaftete Entladevorgang in der Spule ab. Wir würden Spulen benötigen, in denen der Strom verlustfrei weiterfließt, um den Energiespeicher zu einem beliebigen Zeitpunkt anzapfen zu können. Derartige "Supraleiter" funktionieren aber erst bei sehr tiefen Temperaturen und sind uns im Alltag nicht vertraut. Prinzipiell kann man mit derartigen Spulen die gespeicherte Energie genau wie in einem Kondensator beliebig lange speichern. Energie im MagnetfeldFür die Energiedichte an einem beliebigen Punkt in einem Magnetfeld im Vakuum gilt: In Materie gilt für den Fall dass B = μ * H ist (die Materie ist homogen verteilt und linear): Dabei bedeutet:u - magnetische Energiedichte, B - magnetische Flussdichte, μ0 - Permeabilität der Vakuums (=magnetische Feldkonstante), μ - Permeabilität des umgebenden Materials Die gesamte in einem Magnetfeld gespeicherte Energie ergibt sich aus der Summe der Energiedichte der einzelnen Raumpunkte. Aus diesen Zusammenhängen kann abgelesen werden, wann sich die in einem Magnetfeld gespeicherte Energie ändert: 1.) Indem die Energiedichte verändert wird. 2.) Indem das Volumen des Magnetfeldes geändert wird. 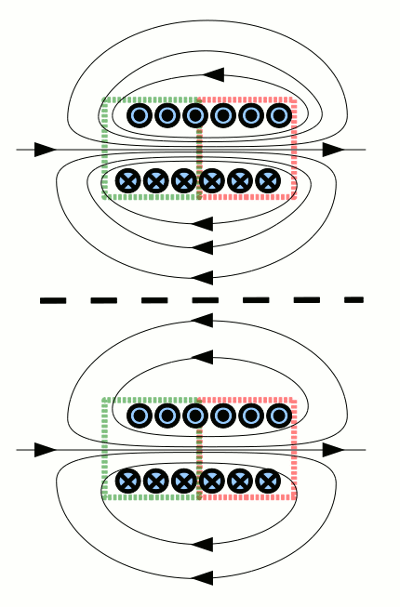
Die in dem Magnetfeld einer Spule gespeicherte Energie nimmt ab, wenn der durch die Windungen der Spule fließende Strom abnimmt. Sichtbar wird das in der Skizze durch die Abnahme der Anzahl der Magnetfeldlinien, die eine Abnahme der Flussdichte anzeigen. Bei diesem Vorgang wird magnetische Energie in elektrische Energie gewandelt. In einer realen Spule wird diese elektrische Energie durch den immer vorhandenen ohmschen Widerstand wiederum in Wärmeenergie verwandelt. 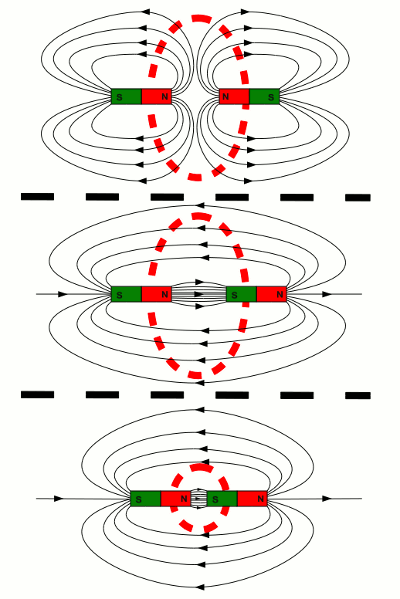
Gesamtenergie der Magnetfelder zweier Permanentmagnete: In der oberen Abbildung stehen die beiden Nordpole der Magnete einander gegenüber, in der mittleren Abbildung je ein Nord- und ein Südpol. Die Dichte der Feldlinien über den gesamten rot umrandeten Bereich ist oben höher als in der mittleren Abbildung. Folglich ist die Gesamtenergie der Magnetfelder zweier Magnete größer, wenn sich gleichnamige Pole gegenüberstehen. Beim Drehen der Magnete von der oberen zur mittleren Abbildung, wird dem Magnetfeld Energie entzogen und in mechanische Energie umgewandelt. Die Magnete richten sich freiwillig mit ihren gegennamigen Polen zueinander aus, wobei mechanische Arbeit verrichtet wird. Zwischen der mittleren und der unteren Abbildung ist der Abstand zwischen den beiden Magneten verringert worden. Dabei erhöht sich die Dichte zwischen den Polen (roter Kreis) zwar geringfügig, das Volumen des Magnetfeldes wird jedoch deutlich verringert. Daher wird der Energiegehalt des Magnetfeldes erneut verringert. Auch beim Annähern der beiden Magnete wird mechanische Arbeit verrichtet, die beiden Magnete ziehen einander an. 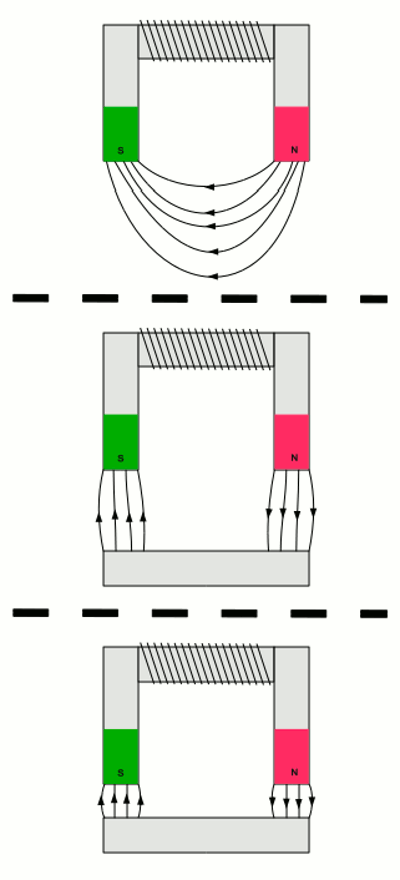
Magnetfeld einer Spule mit U-förmigem Eisenkern: Aufgrund des fließenden Gleichstromes bildet sich ein Magnetfeld ähnlich dem eines U-förmigen Permanentmagneten mit einem Nord- und Südpol. In der mittleren Abbildung befindet sich ein weiterer Eisenkern in einem Abstand zu dem U-Magneten. Dadurch verdichtet sich das Magnetfeld zwischen den Magnetpolen und dem Eisenkern, Das Volumen und somit die Gesamtenergie des Magnetfeldes nimmt jedoch ab. Wird der Eisenkern weiter angenähert, verringert sich das Volumen des Feldes deutlich. Die im Magnetfeld gespeicherte Energie nimmt weiter ab. Dafür steigt die potentielle Energie des gegen die Schwerkraft angehobenen Eisenkerns. <<< Schaltvorgänge Schwingkreise >>> Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum |
|
|