|
|
|
|
News The Project Technology RoboSpatium Contribute Subject index Download Responses Games Gadgets Contact Electric chargeThe video about electrostatic fieldsTerminologyThe electromagnetic force is one of the four fundamental forces in physics. Electromagnetic force is caused by electric charge.Charge quantization is the principle that the charge of any free-standing object is an integer multiple of the elementary charge. By convention, the electric charge of a single electron is -1e which is minus 1.602 * 10 -19 Coulombs. It is the smallest unit for a negative charge carried by an isolated particle. The charge of a particle is only noticeable in the presence of a second charged particle, thus electric fields are usually determined using another, positive charge named test charge. Coulomb force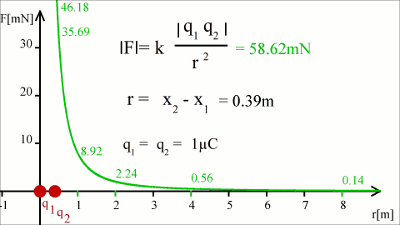
Around 1785 Charles Augustin de Coulomb analyzed the interaction between charged objects and published his findings that are nowadays known as Coulomb's law. "The magnitude of the electrostatic force of interaction between two point charges is directly proportional to the scalar multiplication of the magnitudes of charges and inversely proportional to the square of the distance between them. If the two charges have the same sign, the electrostatic force between them is repulsive; if they have different sign, the force between them is attractive." Thus, the force acting between charged particles depends on the magnitudes of charges, their sign and the distance between them. Charge can be either positive or negative. An object is negatively charged if it has an excess of electrons and is otherwise positively charged or uncharged. The SI derived unit of electric charge is coulomb (C) or ampere-seconds (As), the symbol q or Q is commonly used to denote charges. Charge exhibits electrostatic attraction or repulsion in the presence of other matter. Mathematically we get coulomb's law: Where is: F - Coulomb force q1,2 - charge r - distance k - Coulomb constant = 8.987551787 * 109Vm / As Vectorial notationUsing the vectorial notation we get:Where is: F - Resulting force q1,2 - Charge k - Coulomb constant = 8,987551787 * 109Vm / As r1, r2 - Position vectors of q1 and q2 For the position vectors there is: 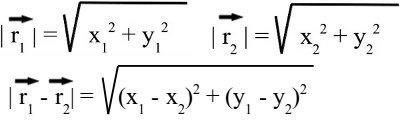 When placing q1 at the point of origin, x1 and y1 are zero, thus the difference of the position vectors is identically to r2. We get the more simple equation of coulomb's law: 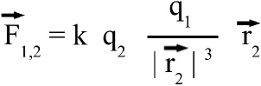 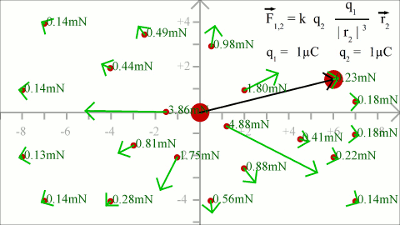
Force between two charged particles in the X/Y plane: At x = 2, y = 1 we get for the magnitude (=length) of r2 a value of xF = k * (q1 * q2)/|r2|3 * x2 = 1.60 and yF = k * (q1 * q2)/|r2|3 * y2 = 0.80 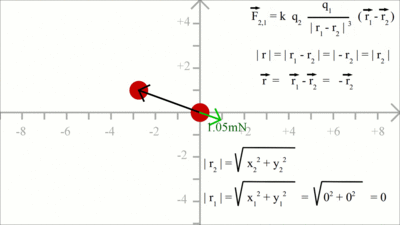
Reaction on the charge placed at the point of origin: In order to get the force acting on charge 1, the position vector 2 has to be subtracted from positiion vector 1. Considering that r1 is still zero, we get -r2 for the distance vector between both charges. We get a force vector with same magnitude, but opposite direction starting at the point of origin. At x = -2.8, y = 1 the magnutude of r2 is xF = k * (q1 * q2)/|r2|3 * (-x2) = 0.96 and yF = k * (q1 * q2)/|r2|3 * (-y2) = -0.34 Electric FieldBy Coulomb's law the force acting on a test charge due to the field of another charge is defined in all points in space. The magnitude of the resulting force depends on the charge of q1 as well as that of q2. When dividing the Coulomb force by the magnitude of the test charge, we get the electric field due to a point charge: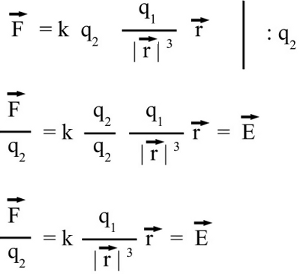 The magnitude of the electric field in a point in space is equivalent to the force acting on a second particle with a charge of one Coulomb, therefore the dimension of the electric field is force per charge, thus Newton per Coulomb. The electric field can be thought of as a function that associates a vector with every point in space, considering the magnitude and the direction. 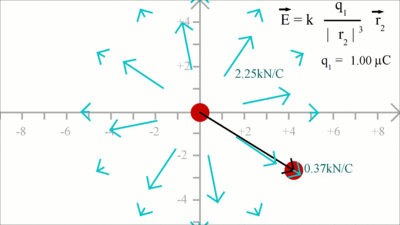
The magnitude of the electric field is constant in all points with constant length of the distance vector: At x = -0.5, y = 2 we get for the magnitude of r: xE = k * (q1)/|r|3 * x2 = -1.53 and yE = k * (q1)/|r|3 * y2 = 2.06 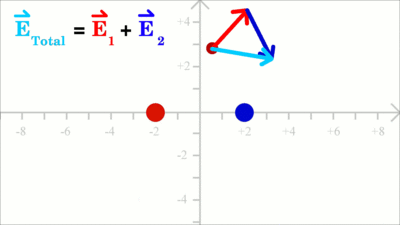
The force acting on a test charge due to a system of point charges is simply the vector addition of the individual forces acting alone on that test charge due to each one of the charges. Considering that the electric field vector is the force vector divided by the magnitude of the test charge, we get two field vectors each caused by one of the two source charges at the drawing shown here (red and blue arrows). The two vectors can be added in head-to-tail fashion to determine the resultant or net electric field vector at that location (light blue arrow). Using this principle, known as the law of superposition we get the electric field vector at any given location surrounding the charges. Uniform Field
An electric field with all vectors having the same magnitude and pointing into the same direction, is named uniform field. Consequently magnitude and direction of the force acting on a test charge placed in a uniform field are invariant in all points in space. An ideal uniform electric field is set up between two parallel plates with infinite dimensions that are oppositely charged, carrying a uniform charge per unit area. As demonstrated in the video, the electric field is nearly uniform between two plates with finite dimensions. Simply keep the distance between the plates small in comparison to their size. Field linesField lines are often used to visualize the direction of force acting on a test charge due to an electric field. A single field line illustrates the path of a positive test charge without mass moving in an electric field.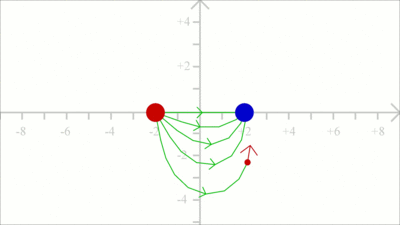
To get the field line pattern, the force acting on a test charge is computed first. Subsequently, the position of the test charge is shifted slightly into the direction of the resulting vector and the force is computed according to the new position. We get a very rough approximation when using a large step width for each iteration as demonstrated at this drawing. 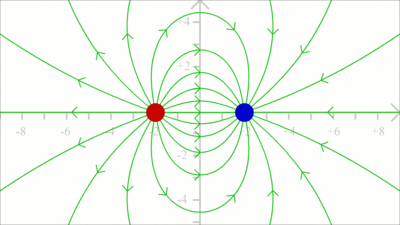
The smaller the step width, the closer the simulation to the real path of a massless test charge. 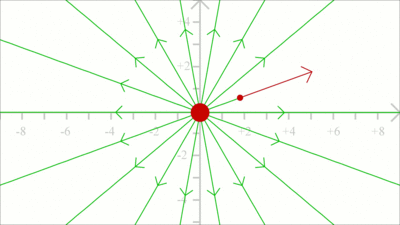
The direction of a field line is defined by the movement of a positive test charge, thus the lines are pointing away from positive charges ... 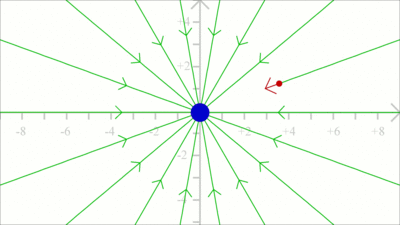
... and to the point of negative charges. Electric dipole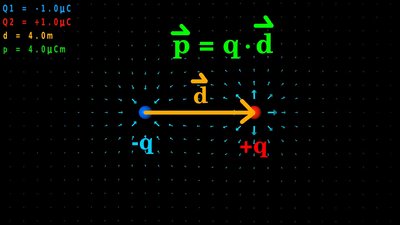
In the simple case of two point charges with a fixed spacing, one with charge -q and the other one with charge +q, there is an electric dipole moment acting on the formation. The arrangement is named electric dipole where d is the displacement vector, ponting from the negative to the positive charge. The electric dipole moment is increasing with increasing magnitude of the charges as well as with increasing space between the particles. The unit of the electric dipole moment is Coulomb times meter or short Coulomb-meter. 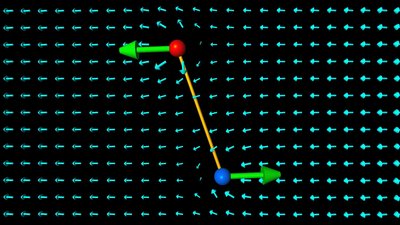
An object with an electric dipole moment is subject to a torque when placed in an external electric field. The dipole is rotating in such a way, that the displacement vector is pointing into the direction of the electric field vectors. The torque is at it's maximum if the axis of the dipole is perpendicular to the direction of the electric field and it becomes zero if the axis is in parallel to those vectors. Coulomb constantThe influence of matter like air on an electric field and so on the force acting between charges is related by the Coulomb constant. That constant is composed of Pi and the relative permittivity of a material, which is the resistance that is encountered when forming an electric field in a medium:Where is: Π - 3.1415927 ε - Permittivity The vacuum permittivity isn't zero, but 8.854 times 10 to -12 As/Vm, thus we get for the Coulomb constant:
Π - 3.1415927 ε0 - Permittivity of vacuum = 8,854188*10-12As/Vm The relative permittivity reflects the effects of a material on an electric field compared to the field in vacuum:
εr - Relative permittivity of the matarial ε - Absolute permittivity of the material ε0 - Permittivity of vacuum We get εr = 1.00059 for gaseous air and caused by the dipole moment and the higher density εr = 80 for liquid water. For Coulomb's law we get:
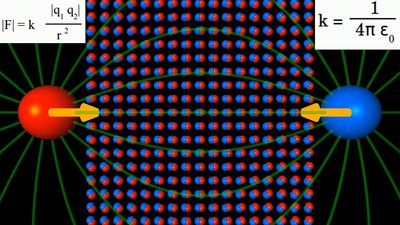
A material with εr > 1, thus with a hight permittivity is placed between a positive and a negative charge. The attracting force between both particles is boosted by the material. 
The repelling force between two positive charges is lowered by the same matarial. The dipoles are arranged in parallel to the field vectors, thus they are pointing tangent to the field lines. electrostatic induction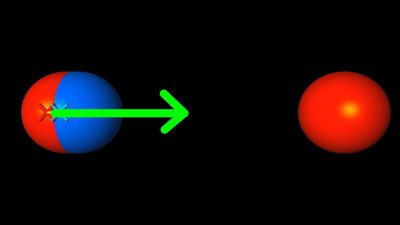
If a positive charge is brought near to an atom or molecule, a dipole is formed due to distortion polarization. The dipole's center of negative charge is pulled to the right, where the positively charged particle is located; In sum there is a force acting on the molecule pointing to the second particle. The lower the distance between both objects, the larger the effect. The redistribution of electrical charge in an object, caused by the influence of nearby charges is named electrostatic induction. 
This effect causes the attraction between light, non conductive objects such as Styrofoam scraps and charged objects such as the electrically charged glass rod. News The Project Technology RoboSpatium Contribute Subject index Archives Download Responses Games Links Gadgets Contact Imprint |
|
|