|
|
|
|
News The Project Technology RoboSpatium Contribute Subject index Download Responses Games Gadgets Contact <<< Voltage Current, resistance and power >>> CapacitorWork inside of an electric fieldAt the previous chapter we have seen that work is performed at charged particles while they are moved against the acing force generated by the electric field. We also recognized "voltage" to be the name of the energy needed to do those work.Metals are materials containing movable charged particles. Attaching voltage to the ends of a conducting wire means exposing the wire to an external electric field lengthwise. The charged particles inside of the wire are dislocated accordant. 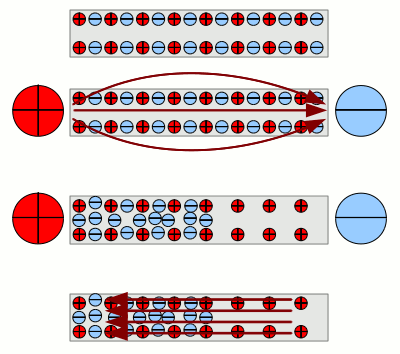
Mock-up of a conducting wire in cross-section. Inside of the wire we see negative charged electrons (blue with minus sign) and positive charged, stationary atomic cores (red with plus sign). If there is no external field, the negative charged electrons and the positive charged atomic cores are arranged homogeneous at the volume of the wire. Attaching voltage to the ends of the wire means exposing the wire to an external electric field (dark red field lines). This is illustrated by the positive respectively negative charge outside of the wire at it's ends The external field generates forces acting on the charged particles inside of the wire. The positive charged atomic cores are stationary and stay at their positions. The electrons start moving to the positive charge of the external field at the right side of the wire. That leads to an inhomogeneous allocation of the charged particles inside of the wire. Inhomogeneous arranged charged particles cause an electric field. This electric field has the same strength as the external field, but points in the opposite direction. As soon as this state is reached, the movement of the electrons stops. The electric field is canceled out inside of the conducting wire. Let's remove the external charges now, meaning reducing the voltage to zero. The only field acting now is the field of the inhomogeneous arranged electrons and atomic cores. It is pointing in the opposite direction of the (now absent) external field. The internal field causes forces acting on the charged particles by now. That results in a movement of the electrons according to the internal field. This movement stops as soon as the electrons are arranged homogeneous around the volume of the wire again. Separation of charge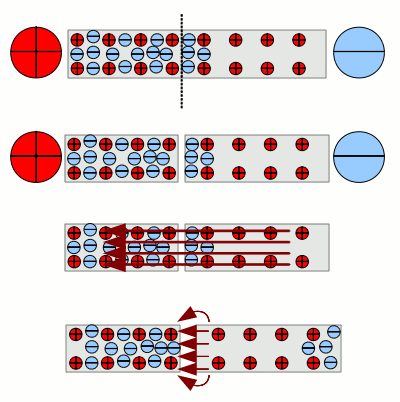
Let's cut the wire into two pieces while the external electric field is still acting and move the pieces slightly apart. What happens if the external field is reduced to zero? Like before, the internal electric field inside of the wire remains and the electrons start moving according to the forces acting. At the cut surface the electrons can't cross over to the right part of the wire. there will remain a spillover of electrons at the left part and a deficit of electrons at the right part of the wire. As a consequence the electric field inside of the wire is not canceled out. Right now it can be detected at the gap between the two pieces of the wire. The force acting on the electrons and atomic cores is assigned to the wire pieces and can be detected, too. The two pieces act similar to macroscopic charged particles. 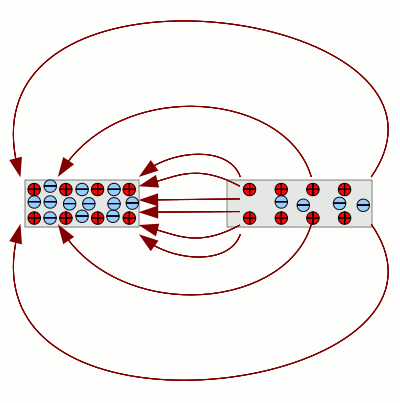
That becomes even more clearly the greater the distance between the parts becomes. The growing distance causes - similar to Coulomb's law - a lower interaction. Inside of the wire parts the electrons start arranging more and more homogeneous. Conducting connection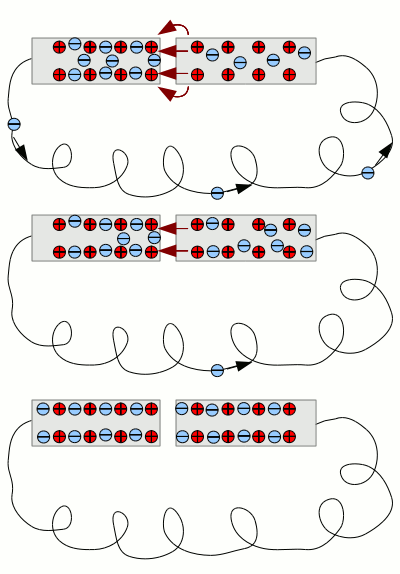
Let's connect the two wire pieces electrically conducting. That doesn't necessarily mean that we have to put them together at the cutting surfaces. We will take another, thin wire and do the connection from the "back" of the pieces. The force acting on the charged particles doesn't point exclusively to the cutting surfaces but also to the "rear" of the pieces. The supernumerary electrons start moving along the thin wire from the left to the right piece. The electric field between the two wire pieces becomes weaker. At the final state as many electrons as atomic cores are in each piece of the wire and the electrons are arranged homogeneous. Energy analysisWhile moving charged particles (electrons) inside of an electric field, energy is converted as we have seen at the previous chapter. The first step was to separate the charged particles inside of the wire by creating an external electric field. Energy was needed to create the external field and to separate the charged particles inside of the wire. Cutting the wire into two pieces did not change the energy of the system. By now we reduced the external field to zero. We needed energy to do so! Reducing the external field to zero means removing the external charges against the attracting force between those charges and the charged particles of the wire! Than we pulled the wire pieces apart. We had to spend energy once again to do so. If we consider the wire pieces to be macroscopic charged particles, we are acting against the attracting force between them.After that, we connected the two pieces by a thin conducting wire. By now the electrons moved according to the force inside the electric field from the left to the right part of the wire. This last step released the energy stored in the system by the previous steps. CapacitorA capacitor is an electronic component being able to store electric charges and thereby electric energy. Capacitors consist of a pair of conducting panels being separated by an insulator. Like at the example mentioned above an arrangement like a capacitor can store electric charges. The separation of the charged particles is done by a voltage source. At the example above we used an external electric field to separate the charges inside of the wire. In reality, "electron pumps" are used to create voltage in electronic circuits. The voltage inside of the circuit is created by "pumping"electrons at one side (=negative terminal) and by "sucking" them out of the circle at the other side (=positive terminal). The electrons are pumped respectively sucked until the according voltage is reached. If a capacitor is connected to a voltage source, electrons are pumped to one panel and they are sucked out of the other plate until the potential between the conducting panels matches those of the voltage source except the different sign (similar to the example above).After disconnecting the voltage source from the capacitor the voltage of the source can still be detected at the terminals. When short circuiting the terminals, electrons from the negative charged panel start flowing to the positive charged panel until the electric field and thereby the voltage between the plates of the conductor becomes zero. 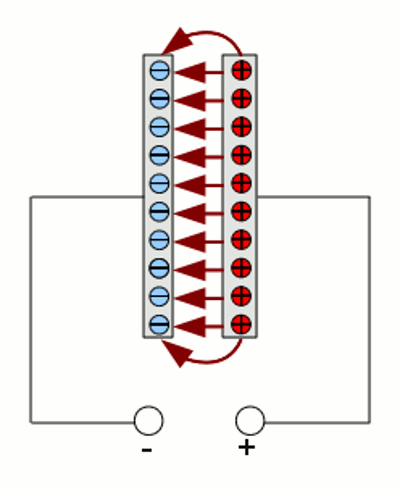
Mock-up of a capacitor: The voltage source pumps electrons to the left side and sucks them away from the right side, leaving the positive charged atomic cores. Between the plates an electric field is created, whose potential corresponds to those of the voltage source with contrary polarity. The smaller the gap between the two plates and the bigger the area of the plates, the more electrons have to be pumped respectively sucked away, until the contrary voltage is reached. The material between the two plates influences the electric field and thereby the number of electrons being pumped, too. For the charge at a given voltage we get: Where is: U - voltage, C - capacitance, Q - charge For the stored energy we get: Where is: W - energy, U - voltage, C - capacitance The factor C gives the capacitance of the capacitor. This is a fixed value given by the construction of the capacitor. The capacitance is influenced by the size of the plates, the distance between the plates and the properties of the insulator material between them. The capacitance is measured in farads. The unit is named after the English physicist Michael Faraday and the symbol F is used for it. The charge stored inside of a capacitor is proportional to the voltage and the stored energy proportional to the square of the voltage. <<< Voltage Current, resistance and power >>> News The Project Technology RoboSpatium Contribute Subject index Archives Download Responses Games Links Gadgets Contact Imprint |
|
|