|
|
|
|
Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Download Reaktionen Spiele Gadgets Kontakt <<< Wechselspannung Schaltvorgänge >>> SelbstinduktionWas kommt zuerst - Strom oder Magnetfeld?Im Kapitel zum Magnetismus haben wir gesehen, dass ein fließender Strom ein Magnetfeld erzeugt und im Kapitel zur Induktion, dass ein sich änderndes Magnetfeld wiederum Spannung und damit Stromfluss bewirkt. Im Kapitel zum Wirbelstrom haben wir die Lenz'sche Regel kennen gelernt, die besagt, dass der induzierte Strom der Änderung eines sich auf- oder abbauenden Magnetfeldes entgegenwirkt. Da beißt sich die Katze doch irgendwie in den Schwanz...Was passiert nun, wenn sich die an eine Spule angelegte Spannung ändert? Lineare Strom- / SpannungsänderungIm Kapitel zu ohm'schen Widerständen haben wir gesehen, dass für diese ein linearer Zusammenhang gilt. Ändert sich die an einem ohm'schen Widerstand anliegende Spannung, so ändert sich der durch diesen fließende Strom proportional dazu: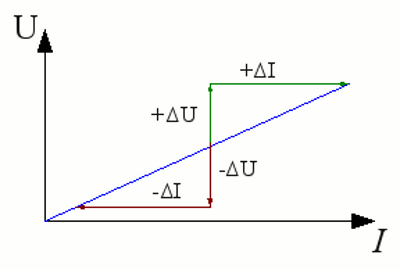
Strom-Spannungs-Diagramm eines ohm'schen Widerstandes. Das Ergebnis ist eine Gerade, deren Steigung dem Widerstandswert entspricht (hohe Steigung = hoher Widerstand). Wird die an dem Widerstand anliegende Spannung um den Wert -ΔU verringert, so verringert sich der fließende Strom um den Wert -ΔI. Umgekehrt erhöht sich der fließende Strom um den Wert +ΔI, wenn die Spannung um +ΔU erhöht wird. Dabei gilt: -ΔU / -ΔI = +ΔU / +ΔI. Der Widerstand eines Kupferdrahtes ist in einem großen Temperaturbereich linear und entspricht damit einem ohm'schen Widerstand. Ändert sich die längs zu einem geraden Kupferdraht anliegende Spannung, so ändert sich auch hier der Stromfluss proportional dazu. Ist der Kupferdraht allerdings zu einer Spule gewickelt, kommt ein weiterer Faktor hinzu: Die Induktionsspannung. Diese ist abhängig von dem sich ändernden magnetischen Fluss durch die von einer Leiterschleife gebildete Fläche und wirkt der Spannungsänderung entgegen. Vom geraden Draht zur SpuleInduktion ist kein Phänomen, das nur in geschlossenen, ringförmigen Leiterschleifen auftritt. Es gilt generell, dass der sich ändernde magnetische Fluss durch eine beliebig geformte Leiterschleife ausschlaggebend für die Höhe der induzierten Spannung ist. Um Spannung in einem Kupferdraht anzulegen, muss dieser mit einer Spannungsquelle elektrisch leitend zu einem Stromkreis verbunden werden. Es handelt sich bei einem Stromkreis, wie der Name vermuten lässt, immer um eine geschlossene Leiterschleife.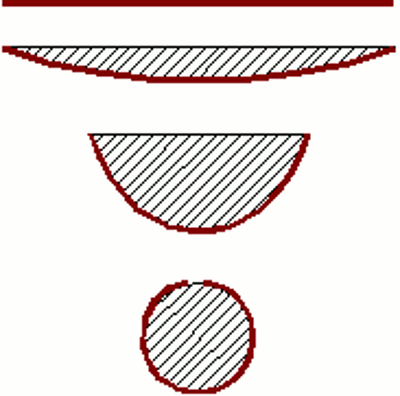
Betrachten wir die von einem Kupferdraht und den Enden des Drahtes gebildete Fläche. Beim geraden Kupferdraht ist diese Fläche Null und erst bei einer leichten Biegung des Drahtes bildet sich eine Fläche zwischen Draht und Drahtenden bis schließlich beim Kreis die Fläche ausschließlich vom Kupferdraht abgegrenzt wird. In der Skizze ist die Fläche, die von dem halbkreisförmigen Draht gebildet wird, am größten. Ist hier die stärkste Selbstbeeinflussung bei gegebener Drahtlänge zu erwarten? Nein! Denn wir dürfen die Drahtlänge der Zu- und Ableitung nicht vernachlässigen! Es gilt die Leiterschleife des gesamten Stromkreises zu beachten. Hier schneidet der Kreis am besten ab. Bei diesem ist das Verhältnis von Umfang zur Innenfläche am größten. InduktivitätBei gegebener, fester Spulengeometrie hängt die induzierte Spannung von der Permeabilität des umgebenden Materials ab. Im Kapitel zur Hysterese haben wir gesehen, dass diese nicht nur vom Material, sondern auch von dessen magnetischer Vorgeschichte abhängt. Gehen wir vereinfachend von einem konstanten Wert für die Permeabilität aus, so erhalten wir für den magnetischen Fluss:Dabei bedeutet: Φ - magnetischer Fluss, N - Anzahl Spulenwicklungen, L - Induktivität, I - Stromstärke Der von einer Spule erzeugte magnetische Fluss ist also proportional zum fließenden Strom und umgekehrt proportional zur Anzahl der Windungen. Der Proportionalitätsfaktor wird als die Induktivität der Spule bezeichnet. Das Formelzeichen lautet L und die Einheit lautet Henry, benannt nach dem US-amerikanischen Physiker Joseph Henry. Abgekürzt wird die Einheit mit dem Buchstaben H. Eine Induktivität von einem Henry liegt vor, wenn bei einer Stromänderung von einem Ampere pro Sekunde eine Selbstinduktionsspannung von einem Volt entsteht. Zusammen mit dem Induktionsgesetz ergibt sich für die induzierte Spannung einer Spule: Dabei bedeutet: Φ - magnetischer Fluss, N - Anzahl Spulenwicklungen, L - Induktivität, I - Stromstärke, ε - induzierte Spannung Die induzierte Spannung ist also proportional zur Stromänderung pro Zeitintervall. Anlegen einer Spannung an eine Spule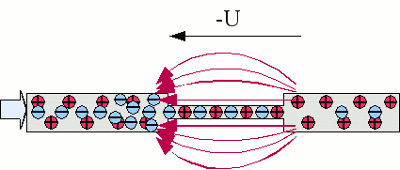
Schließt man einen ohmschen Widerstand an eine Spannungsquelle an, so baut sich in dem Widerstand ein elektrisches Feld auf, das wiederum eine Gegenspannung bewirkt, die vom Betrag her gleich groß, aber genau entgegengesetzt zur angelegten Spannung ist. Vorstellen kann man sich das Entstehen dieser Gegenspannung dadurch, dass sich die Elektronen vor dem Widerstand "stauen", während diese hinter dem Widerstand "abgesaugt"werden. Der Ohmsche Widerstand entspricht einer "Engstelle" im Stromkreis. Schließt man eine Spule aus einem widerstandslosen Leitermaterial an eine Spannungsquelle an, so beginnt ein Strom zu fließen. Der sich ändernde Stromfluss induziert eine Spannung die gleich groß, aber entgegengesetzt zur angelegten Spannung ist. Der Anstieg der Stromstärke bleibt über die Zeit konstant, d.h. es fließt ein stetig wachsender Strom. Die Zunahme der Stromstärke hängt lediglich von der angelegen äußeren Spannung und der Induktivität der Spule ab. Dabei wächst die Stromstärke gegen Unendlich (der Draht hat keinen Widerstand). Wie bereits oben angedeutet, besitzt der in Spulen zumeist eingesetzte Kupferdraht bei den Einsatztemperaturen eines Elektrofahrzeugs einen ohmschen (=linearen) Widerstand. Für den Stromfluss einer realen, mit einem ohmschen Widerstand behafteten Spule ergibt sich für die Funktion von Strom und Zeit: Dabei bedeutet: I - Strom, U0 - angelegte Spannung, R - ohmscher Widerstand des Spulendrahtes, e - Eulersche Zahl, t - Zeit, L - Induktivität 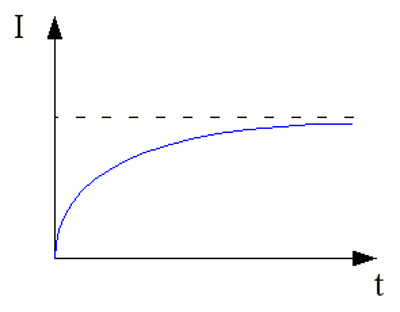
Beim Anschließen einer Spule an eine Gleichspannungsquelle fließt zum Zeitpunkt des Anschließens kein Strom. Dieser steigt danach auf einen Endwert, der vom ohmschen Widerstand des verwendeten Spulendrahtes abhängt. Der Endwert errechnet sich zu <<< Wechselspannung Schaltvorgänge >>> Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum |
|
|