|
|
|
|
Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Download Reaktionen Spiele Gadgets Kontakt <<< Leistungsbilanzen Spannung >>> Elektrische LadungDas Video zur ElektrostatikBegriffsdefinitionDie elektromagnetische Wechselwirkung ist eine der vier Grundkräfte der Physik. Die Ursache elektromagnetischer Wechselwirkung ist elektrische Ladung.Ladung kann nur als ganzzahliges Vielfaches der Elementarladung e auftreten. Der bekannteste Träger der negativen Elementarladung ist das Elektron. Unter der Voraussetzung, dass Elektronen nicht aufgespalten werden können (wofür es bislang keinen Nachweis gibt), ergibt sich automatisch, dass nur ganzzahlige Vielfache der Elektronenladung von eben diesen Elektronen übertragen werden können. Ladung wird nach dem SI-System in der Einheit Coulomb angegeben. 1e entspricht circa 1,602 * 10-19Coulomb. Da sich die Ladung eines Teilchens nur in Anwesenheit zumindest eines weiteren Teilchens bemerkbar macht, werden elektrische Felder üblicherweise mit Hilfe einer positiven Ladung, die als Probeladung bezeichnet wird, untersucht. Coulomb Kraft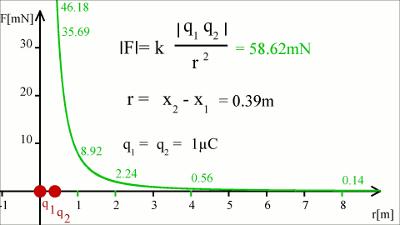
Um 1785 veröffentlichte Charles Augustin de Coulomb nach umfangreichen Experimenten zu elektrischen Ladungen das später nach ihm benannte Coulombsche Gesetz: "Der Betrag der Kraft zwischen zwei geladenen Kugeln ist proportional zum Betrag des Produkts der beiden Ladungsmengen und umgekehrt proportional zum Quadrat des Abstandes der Kugelmittelpunkte. Haben beide Ladungen das gleich Vorzeichen, so besteht eine abstoßende Kraftwirkung, andernfalls ist diese anziehend." Die zwischen Ladungen wirkenden Kräfte werden also von der Ladungsmenge, dem Abstand und dem Vorzeichen bestimmt. Elektrische Ladung kann positive und negative Werte annehmen. Die Zuordnung der Vorzeichen erfolgt willkürlich. Dabei wird z.B. die Elektronenladung üblicherweise als negative Ladung gesetzt, woraus sich ergibt, dass Protonen positive Ladung tragen. Die Einheit für die elektrische Ladung ist Amperesekunden (Einheitenzeichen As) oder Coulomb (Einheitenzeichen C), als Formelzeichen wird q oder Q verwendet. Ladungen machen sich durch die zwischen ihnen wirkenden Kräfte bemerkbar. Mathematisch lautet das Coulombsche Gesetz wie folgt: Dabei bedeutet: F - Resultierende Kraft q1,2 - Ladungsmenge r - Abstand k - Coulomb-Konstante = 8,987551787 * 109Vm / As Vektorielle SchreibweiseIn der vektoriellen Schreibweise lautet das Coulombsche Gesetz wie folgt:Dabei bedeutet: F - Resultierende Kraft q1,2 - Ladungsmenge k - Coulomb-Konstante = 8,987551787 * 109Vm / As r1, r2 - Ortsvektoren von q1 und q2 Für die beiden Ortsvektoren gilt:  Wird q1 in den Koordinatenursprung gesetzt, so werden x1 und y1 zu Null und die Differenz der Ortsvektoren ist identisch zu r2. Wir erhalten die vereinfachte Form des Coulombschen Gesetzes: 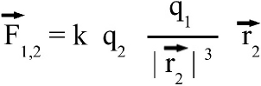 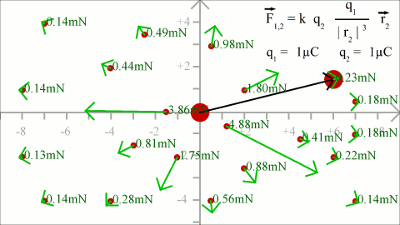
Kraftwirkung zwischen zwei Punktladungen in einer zweidimensionalen Ebene: Im Punkt x = 2, y = 1 ergibt sich für den Betrag (=die Länge) von r2 ein Wert von xF = k * (q1 * q2)/|r2|3 * x2 = 1.60 und yF = k * (q1 * q2)/|r2|3 * y2 = 0.80 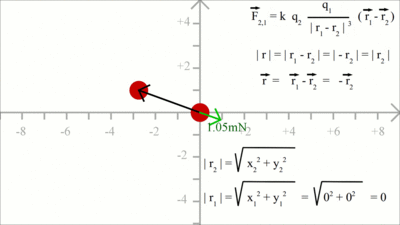
Gegenkraft auf die Ladung im Koordinatenursprung: Zur Berechnung der Kraft auf Ladung 1 muss der Richtungsvektor 2 von Richtungsvektor 1 abgezogen werden. Da Ladung 1 nach wie vor im Koordinatenursprung sitzt und somit r1 Null bleibt, ist der resultierende Richtungsvektor -r2. Es ergibt sich eine Kraft gleichen Betrags, aber mit im Vergleich zu r2 entgegengesetzter Richtung, die im Koordinatenursprung angreift. Im Punkt x = -2.8, y = 1 ergibt sich für den Betrag von r2 ein Wert von xF = k * (q1 * q2)/|r2|3 * (-x2) = 0.96 und yF = k * (q1 * q2)/|r2|3 * (-y2) = -0.34 Elektrische FeldstärkeIm Feld einer Punktladung q1 wirkt auf eine zweite Ladung q2 die durch das Coulombsche Gesetz beschriebene Kraft. Der Betrag der Kraft ist dabei abhängig sowohl von der Ladung q1 als auch von der Ladung von q2. Dividieren wir die auf die Probeladung q2 wirkende Kraft durch deren Ladung, so erhalten wir die von der Ladung im Koordinatenursprung verursachte elektrische Feldstärke: Die elektrische Feldstärke gibt also an, welche Kraft pro einem Coulomb Ladung in einem Punkt des Feldes ausgeübt wird. Diese ist wie die Coulomb-Kraft ein Vektor, berücksichtigt also neben dem Betrag auch die Richtung. Als Einheit der elektrischen Feldstärke ergibt sich Kraft pro Ladung, also Newton pro Coulomb. 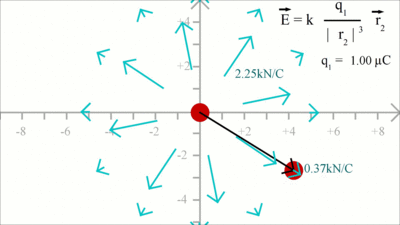
Bei gleichem Abstand vom Zentrum ergibt sich für eine punktförmige Ladung ein gleicher Betrag für die elektrische Feldstärke: Im Punkt x = -0.5, y = 2 ergibt sich für den Betrag von r ein Wert von xE = k * (q1)/|r|3 * x2 = -1.53 und yE = k * (q1)/|r|3 * y2 = 2.06 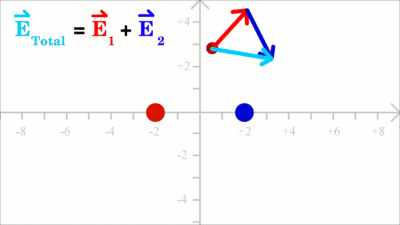
Die elektrische Feldstärke in einem Punkt im Feld mehrerer Punktladungen ergibt sich durch Addition der Feldstärkevektoren aller Ladungen. Nach der Berechnung des Vektors für die positive Ladung (roter Vektor) erfolgt in der Darstellung die Berechnung für die negative Ladung (blauer Vektor). Wird der Startpunkt des zweiten Vektors an den Endpunkt des ersten Vektors verschoben, so wird die Summe durch einen Vektor vom Startpunkt des ersten zum Endpunkt des zweiten Vektors dargestellt (hellblauer Vektor). Nach diesem Verfahren, dass man als Superpositionsprinzip bezeichnet, kann die elektrische Feldstärke in jedem Punkt des Raumes um die beiden Ladungen errechnet werden. Homogenes Feld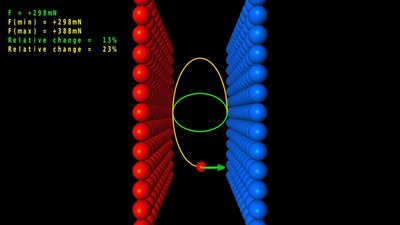
Ein elektrisches Feld, in dem der Feldstärkevektor in allen Punkten in die gleiche Richtung zeigt und den gleichen Betrag besitzt, bezeichnet man als homogenes elektrisches Feld. Entsprechend ist in einem derartigen Feld die Kraft auf eine Probeladung in allen Punkten gleich groß und zeigt in die gleiche Richtung. Rein mathematisch erhält man ein derartiges Feld zwischen zwei unendlich ausgedehnten planparallelen Platten mit Ladungen gleichen Betrags, aber unterschiedlichen Vorzeichens. Wie im Video gezeigt, erhält man ein annähernd homogenes Feld auch zwischen zwei Platten endlicher Ausdehnung. Je kleiner der Abstand der Platten im Verhältnis zu deren Ausdehnung, um so näher ist das elektrische Feld im Kernbereich an einem idealen homogenen Feld. FeldlinienUm elektrostatische Felder zu visualisieren, werden häufig Feldlinien gezeichnet, welche die von einer oder mehreren Ladungen in einem Punkt ausgeübte Kraftrichtung veranschaulichen. Die Feldlinie zeichnet den Weg, entlang dessen sich eine positive Probeladung ohne Berücksichtigung von Massenträgheit oder Beschleunigungseffekten bewegt.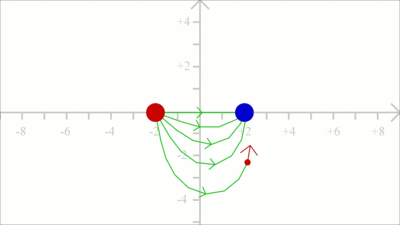
Das Feldlinienbild kann konstruiert werden, indem der Kraftvektor auf eine Probeladung in einem Punkt des Feldes berechnet wird. Die Probeladung wird anschließend ein kleines Wegstück längs der Richtung dieses Kraftvektors bewegt und die Berechnung der Kraft erneut durchgeführt. Die Schrittweite sollte nicht so groß wie in der Darstellung links gewählt werden gewählt werden. 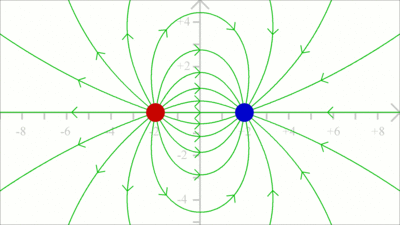
Je kleiner diese ausfällt. um so näher ist die Rechnung an der tatsächlichen Bahn einer masselosen Probeladung. 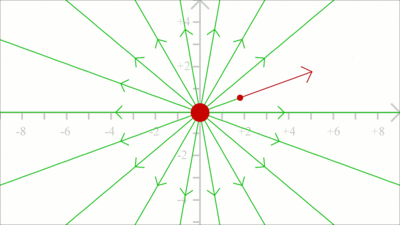
Die Richtung der Feldlinien wird von der Bewegung der positiven Probeladung vorgegeben. Diese zeigen folglich immer von einer positiven Ladung weg... 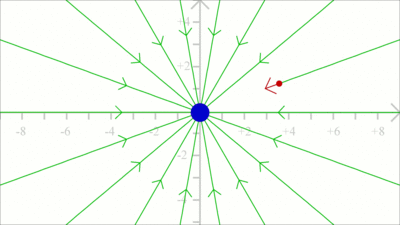
... und hin zu einer negativen Ladung. Elektrisches Dipolmoment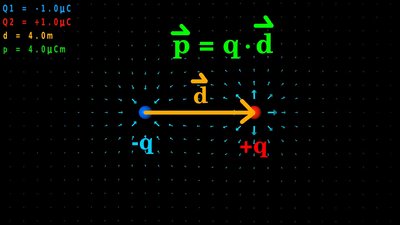
Befindet sich zu einer negativen Ladung -q im Abstand d eine dem Betrag nach gleich große positive Ladung +q und sind diese Ladungen untereinander starr verbunden, so besitzt diese Struktur ein Dipolmoment. Die Anordnung bezeichnet man auch kurz als elektrischen Dipol. Das Dipolmoment steigt sowohl wenn der Betrag der Ladungen erhöht wird, als auch bei konstanter Ladung mit zunehmendem Abstand zwischen den Ladungen. Als Einheit für das elektrische Dipolmoment ergibt sich in SI-Einheiten Coulomb mal Meter, kurz Coulomb-Meter. 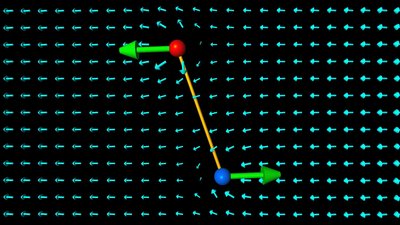
Befindet sich ein elektrischer Dipol in einem äußeren elektrischen Feld, so wirkt ein Drehmoment auf die Anordnung. In einem homogenen Feld richtet sich dieser mit seiner Achse parallel zu den Feldvektoren aus. Das Drehmoment ist maximal, wenn die Achse des Dipols senkrecht zu den Vektoren des äußeren Feldes steht und dieses wird Null, wenn die Achse parallel dazu ausgerichtet ist. Coulomb-KonstanteDer Einfluss von Materie - wie zum Beispiel von Luft - auf die elektrische Feldstärke und somit auf die Kraftwirkung zwischen Ladungen wird im Coulomb-Gesetz durch die Konstante k berücksichtigt. Diese setzt sich aus Pi und der Permittivität, also der Durchlässigkeit des jeweiligen Materials für elektrische Felder zusammen, die üblicherweise durch den Buchstaben Epsilon repräsentiert wird:Dabei bedeutet: Π - 3.1415927 ε - Permitivität des umgebenden Materials Für das Vakuum ist die Coulomb-Konstante nicht Null:
Π - 3.1415927 ε0 - Permitivität des Vakuums = 8,854188*10-12As/Vm Die relative Permittivität gibt die feldändernden Effekte eines Materials im Vergleich zum Vakuum an:
εr - Relative Permitivität des Materials ε - Absolute Permitivität des Materials ε0 - Permitivität des Vakuums In Luft erhalten wir 1,00059 für εr, in flüssigem Wasser ergibt sich ein Wert von 80 - auch hier macht sich der Dipolcharakter der Wassermoleküle bemerkbar. Damit ergibt sich das Coulombsche Gesetz zu:
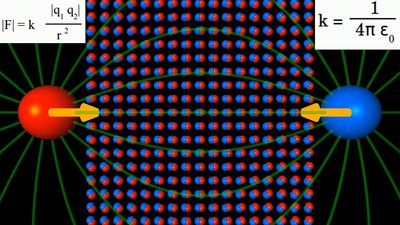
Zwischen einer positiven und einer negativen Ladung befindet sich ein Material mit einem hohen Wert für εr, also einer hohen Durchlässigkeit für elektrische Felder. Die anziehende Kraftwirkung zwischen beiden Ladungen wird durch das Material erhöht. 
Die abstoßende Kraft zwischen zwei positiven Ladungen wird durch das gleiche Material hingegen deutlich verringert. Zu sehen ist, dass sich die Dipole längs der Feldlinien, also in Richtung der Feldstärkevektoren ausrichten. Influenz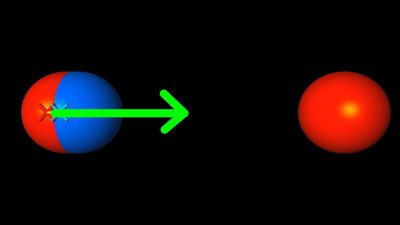
Nähert sich ein elektrisch neutrales Atom oder Molekül einer positiven Ladung, so kommt es durch Verschiebungspolarisation zur Ausbildung eines Dipols. Der negative Ladungsschwerpunkt des Dipols ist der positiven Ladung zugewandt, wodurch in dem inhomogenen Feld eine Kraftwirkung in Richtung der positiven Ladung entsteht. Der Effekt ist größer, je geringer der Abstand zwischen Dipol und Ladung wird. Die räumliche Verschiebung elektrischer Ladungen durch Einwirkung eines elektrischen Feldes bezeichnet man als Influenz. 
Dieser Effekt bewirkt, dass elektrisch neutrale Körper wie diese Styroporschnipsel von geladenen Objekten angezogen werden. <<< Leistungsbilanzen Spannung >>> Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum |
|
|