|
|
|
|
Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Download Reaktionen Spiele Gadgets Kontakt <<< Spannungsteiler Kippstufen >>> RC-GliedDas Video zu RC-GliedernKondensator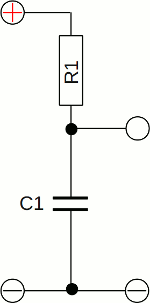 RC-Glied steht für Resistor-Capacitor, also Widerstand-Kondensator Schaltung. Das einfachste RC-Glied besteht aus einer Reihenschaltung eines Widerstands und eines Kondensators. Wird dieser Schaltkreis an eine konstante Spannung angeschlossen, so hängt der Spannungsverlauf am Kondensator von der Kapazität und dem Widerstand des Gesamtstromkreises ab (siehe Kapitel Schaltvorgänge):
RC-Glied steht für Resistor-Capacitor, also Widerstand-Kondensator Schaltung. Das einfachste RC-Glied besteht aus einer Reihenschaltung eines Widerstands und eines Kondensators. Wird dieser Schaltkreis an eine konstante Spannung angeschlossen, so hängt der Spannungsverlauf am Kondensator von der Kapazität und dem Widerstand des Gesamtstromkreises ab (siehe Kapitel Schaltvorgänge):[3.32] 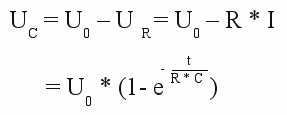 Dabei bedeutet: UC - Spannungsabfall am Kondensator, UR - Spannungsabfall am Widerstand, U0 - Eingangsspannung, I - Gesamtstrom, Q - Ladung, C - Kapazität, R - Widerstand, t - Zeit, e - Eulersche Zahl 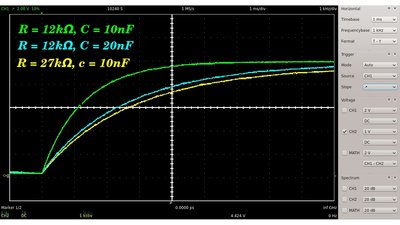
Der Spannungsabfall am Kondensator strebt dem Wert der konstanten Eingangsspannung entgegen. Je höher der Widerstand beziehungsweise die Kapazität, um so niedriger ist die Spannung am Kondensator nach einer festen Zeitspanne. Der Anstieg des Signals ist zu Beginn des Ladevorgangs am höchsten. 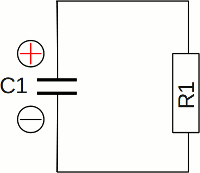 Fällt die Eingangsspannung auf Null Volt (z. B. weil die Eingangsklemmen kurzgeschlossen werden, entlädt der Kondensator die in ihm gespeicherte Energie über den Widerstand. Ein Ersatzschaltbild des kurzgeschlossenen RC-Gliedes besteht aus einer Parallelschaltung eines geladenen Kondensators und eines Widerstands.
Fällt die Eingangsspannung auf Null Volt (z. B. weil die Eingangsklemmen kurzgeschlossen werden, entlädt der Kondensator die in ihm gespeicherte Energie über den Widerstand. Ein Ersatzschaltbild des kurzgeschlossenen RC-Gliedes besteht aus einer Parallelschaltung eines geladenen Kondensators und eines Widerstands.
Die Funktion der Spannung in Abhängigkeit der Zeit ist wie folgt: 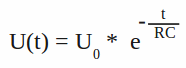 Dabei bedeutet: U0 - Spannungsabfall am Kondensator bei t=0 C - Kapazität, R - Widerstand, t - Zeit, e - Eulersche Zahl Die Zeitspanne die benötigt wird, um die Spannung auf [9.1] τ = R * C Dabei bedeutet:τ - RC Zeitkonstante R - Widerstand C - Kapazität 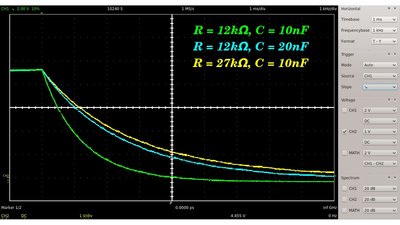
Wird der Kondensator entladen, so fällt die Spannung von ihrem Ausgangswert auf Null. Je höher der Widerstand beziehungsweise die Kapazität, um so höher ist die Restspannung am Kondensator nach einer festen Zeitspanne. Erneut ist die Änderungsrate des Signals zu Beginn des Vorgangs am Höchsten. Widerstand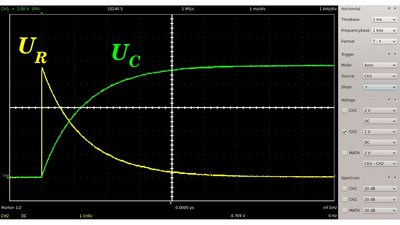
In einem linearen RC-Glied entspricht die Summe der Spannungen am Widerstand und am Kondensator der Eingangsspannung ( 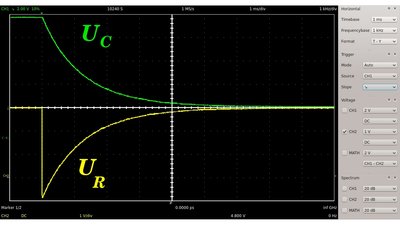
Fällt die Eingangsspannung auf Null Volt, so wird der Kondensator entladen. Wie beim Laden ist der Strom durch den Schaltkreis zu Beginn des Vorgangs am höchsten (t=0). Nun entspricht die Spannung am Kondensator der am Widerstand, abgesehen vom Vorzeichen. Der Kondensator fungiert als Spannungsquelle des Schaltkreises (siehe Ersatzschaltbild weiter oben). Theoretisch dauert der Lade- beziehungsweise Entladevorgang unendlich lange, aber in der Praxis kann man nach einer gewissen Zeitspanne keine von Null beziehungsweise von der Eingangsspannung verschiedene Spannung mehr feststellen. Daher verwenden man die Zeitspanne, die benötigt wird, bis die Spannung auf einen Wert von der ursprünglichen Spannung geteilt durch die Eulersche Zahl gefallen ist, um ein RC-Glied zu charakterisieren. Siehe die Definition der Zeitkonstante weiter oben. Rechtecksignal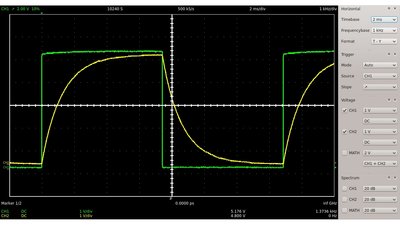
Wird das RC-Glied an eine Rechteckspannung angeschlossen, so wird der Kondensator periodisch ge- beziehungsweise entladen. 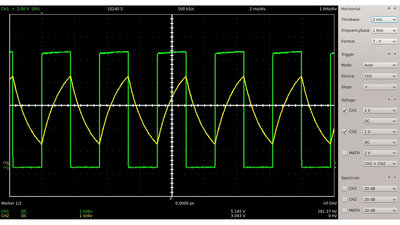
Außer der Kapazität und dem Widerstand, beeinflusst auch die Schaltfrequenz der Eingangsspannung die maximale Spannung am Kondensator. Je geringer die Schaltfrequenz, um so höher ist die Spitzenspannung. 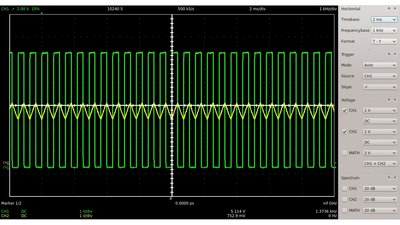
Mit zunehmender Schaltfrequenz kann nahezu keine Zusätzliche Ladung in den Kondensator fließen beziehungsweise diesen verlassen. Die Spannung tendiert zur Hälfte der Spitzenspannung der symmetrischen Rechteckspannung am Eingang des Schaltkreises. Die folgenden Oszillogramme zeigen das Signal am Widerstand bei Anliegen einer Rechteckspannung: 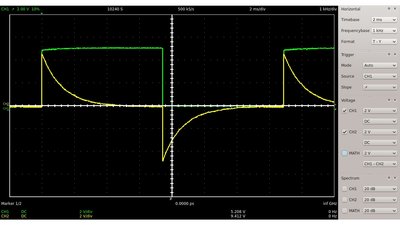
Wie zu sehen, ändert sich das Vorzeichen der anliegenden Spannung während der Kondensator ge- beziehungsweise entladen wird. 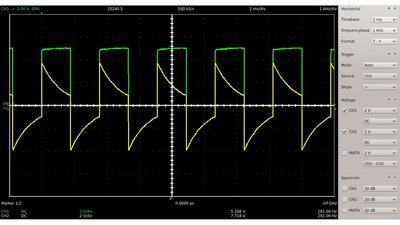
Wie am Kondensator sinkt auch die Spitzenspannung am Widerstand mit zunehmender Schaltfrequenz. 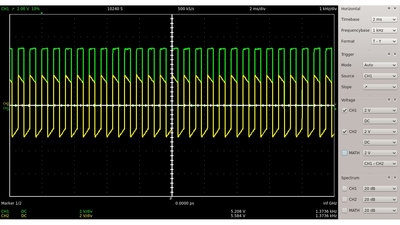
Jedoch steigt die Effektivspannung mit zunehmender Schaltfrequenz. Diese wird durch die von der Kurve und der X-Achse begrenzte Fläche repräsentiert. Sinusförmige Eingangsspannung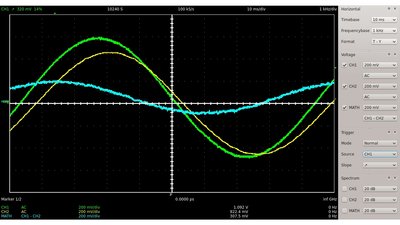
Wie bei der Rechteckspannung sinkt auch beim Anlegen einer sinusförmigen Eingangsspannung die Spitzenspannung am Kondensator mit zunehmender Frequenz - die am Widerstand steigt jedoch. UEingang(Grün), UWiderstand(Blau) und UKondensator(Gelb). 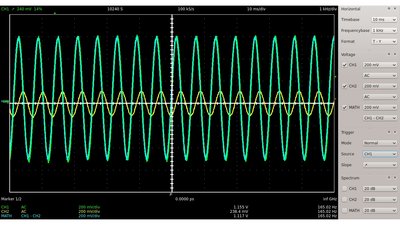
Wird die Ausgangsspannung am Kondensator abgegriffen, können niedrige Frequenzen den Schaltkreis passieren, während hohe Frequenzen blockiert werden. Der Schaltkreis verhält sich wie ein Tiefpass. Wird die Ausgangsspannung hingegen am Widerstand abgegriffen, so können hohe Frequenzen den Schaltkreis passieren, während tiefe Frequenzen blockiert werden. Nun verhält sich die Schaltung wie ein Hochpass. Die Frequenz, ab der die Spannung am Ausgang auf Dabei gilt: f - Grenzfrequenz R - Widerstand C - Kapazität Neben der Amplitude variiert auch die Phase, also die Zeitpunkte der Nulldurchgänge des Ausgangssignals am Widerstand und des Eingangssignals mit variierender Frequenz. Der sich ergebende Phasenwinkel errechnet sich zu: Dabei bedeutet: α - Phasenwinkel f - Frequenz R - Widerstand C - Kapazität Für den sich ergebenden Phasenwinkel gilt: 0° < α < 90° 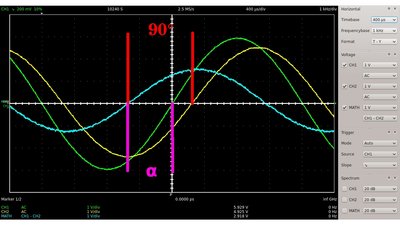
Zwischen dem Ausgangssignal am Kondensator und dem am ohmschen Widerstand besteht in einem linearen RC-Glied ein Phasenwinkel von 90°. Erinnert euch daran, dass der Stromfluss durch den Schaltkreis dann am höchsten ist, wenn die Änderungsrate der Spannung am Kondensator ihren Maximalwert erreicht. F = 312.5Hz, C = 0.1μF, R = 2.7kΩ UEingang(Grün), UWiderstand(Blau) und UKondensator(Gelb). Der Phasenwinkel zwischen Eingangsspannung und Strom (=Spannungsabfall am Widerstand) ändert sich mit der Eingangsfrequenz. 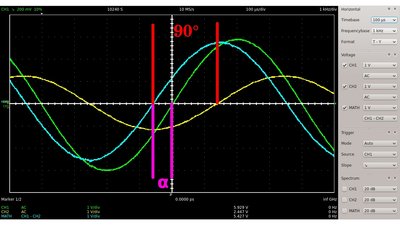
F = 1250.0Hz, C = 0.1μF, R = 2.7kΩ UEingang(Grün), UWiderstand(Blau) und UKondensator(Gelb). Je höher die Frequenz des Eingangssignals, um so kleiner der Winkel zwischen Strom und Spannung des Eingangssignals. Bandpass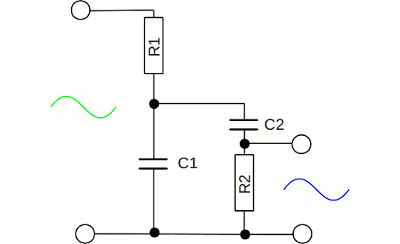
Wird ein Hochpass an die Ausgangsklemmen eines Tiefpasses angeschlossen (oder umgekehrt ein Tiefpass an einen Hochpass), lässt der Gesamtschaltkreis nur noch eine bestimmte Bandbreite an Frequenzen passieren, während alle anderen Frequenzen abgeschwächt werden. Einen derartigen Schaltkreis bezeichnet man als Bandpass. 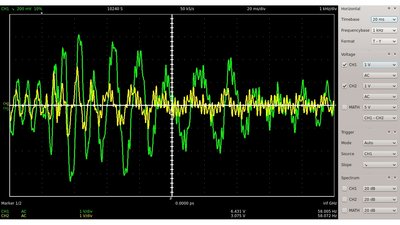
Eine verbreitete Anwendung finden derartige Schaltkreise in der Audiosignalbearbeitung. Durch Verwendung mehrerer derartiger Filter in Verbindung mit Verstärkerschaltkreisen, kann die Balance zwischen verschiedenen Frequenzen eines elektronischen Signals verändert werden. Ein Equalizer wird verwendet, um bestimmte Frequenzbänder zu verstärken beziehungsweise abzuschwächen. Das Oszillogramm zeigt das Eingangssignal (Grün) und das Ausgangssignal (Gelb) eines Audiosignals, das durch einen kombinierten Tief- und Hochpass gefiltert wurde. <<< Spannungsteiler Kippstufen >>> Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum |
|
|