|
|
|
|
Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Download Reaktionen Spiele Gadgets Kontakt <<< Arbeit, Energie, Leistung Fahrzeugauslegung >>> DrehmomentKraftKraft ist eine gerichtete physikalische Größe. Sie ist die Ursache für die Beschleunigung oder Verformung von Körpern.Auf der Erdoberfläche allgegenwärtig ist die Gewichtskraft. Sie zieht alle mit Masse ausgestatteten Gegenstände in Richtung Erdmittelpunkt. Befindet sich der Gegenstand im ungebremsten (=freien) Fall, so beschleunigt dieser konstant in Richtung des Erdmittelpunktes. Spätestens an der Erdoberfläche endet der freie Fall, denn hier wirkt die Normalkraft der Gewichtskraft entgegen. Die Normalkraft hat ihre Ursache in der Verformung der Erdoberfläche, die ihrerseits Druckkräfte hervorrufen, wie auch eine Feder beim Zusammendrücken entsprechende Gegenkräfte erzeugt. Ruht ein Gegenstand auf der Erdoberfläche, so sind Gewichts- und Normalkraft gleich groß, wirken aber in exakt entgegengesetzter Richtung. Betrachten wir einen ausgedehnten (nicht punktförmigen) Gegenstand, so greift die Gewichtskraft (genau genommen die Summe der Gewichtskräfte) im Schwerpunkt des Gegenstandes an, die Normalkraft jedoch am Auflagepunkt. Wirken beide Kräfte nicht in Richtung der Verbindungslinie der beiden Punkte, so wirkt ein DrehmomentAls Drehmoment wird ein Kräftepaar bestehend aus zwei parallelen Kräften mit entgegengesetzter Richtung bezeichnet, das einen Körper in Rotation versetzt oder verbiegt (tordiert).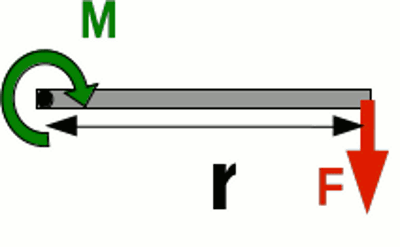
Ist ein Körper an einer Achse drehbar gelagert, so gilt für das Drehmoment: Dabei bedeutet: M - Resultierendes Drehmoment, r - Abstand Drehachse zu Angriffspunkt der Kraft (Hebelarm), F - Kraft senkrecht zum Hebelarm 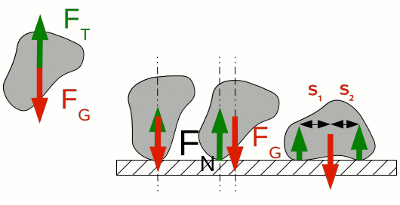
Links im Bild befindet sich der Stein im freien Fall. Gewichts- und Trägheitskraft greifen im Schwerpunkt des Körpers in entgegengesetzter Richtung an. Die Summe der Kräfte ist Null und es wird kein Drehmoment erzeugt. Liegt der Stein auf einer Auflagefläche auf, so verhindert die Normalkraft den Fall des Steines. Die Normalkraft greift am Auflagepunkt des Steines an und wirkt senkrecht zur Auflagefläche nach oben. Die Gewichtskraft greift weiterhin im Schwerpunkt des Steines an. Befindet sich der Schwerpunkt genau auf der Senkrechten zum Auflagepunkt, wirkt kein Drehmoment und der Stein verharrt in seiner Position. Dieser Zustand ist rein theoretischer Natur, denn weichen Auflage- und Schwerpunkt auch nur seeeeeehr gering von besagter Senkrechten ab, beginnt das resultierende Drehmoment den Stein zu kippen. Kein Stein bleibt auf seiner Spitze liegen. Ganz rechts im Bild ist der Stein zur Seite gekippt und liegt auf zwei Punkten auf. Entsprechend wirken in beiden Auflagepunkten Normalkräfte senkrecht nach oben. Die Gewichtskraft wirkt weiterhin ausgehend vom Schwerpunkt senkrecht nach unten. Die Summe der Beträge der beiden Auflagekräfte (FN1 und FN2) ergibt den Betrag der Gewichtskraft (FG) und die Summe der Drehmomente ergibt Null. Der Stein befindet sich in einer stabilen Lage. In der Skizze nur zweidimensional abgebildet, ist ein reeller Stein natürlich dreidimensional. Entsprechend kommt ein dritter Auflagepunkt hinzu. Auch für die drei Punkte gilt, dass die Summe aus Normalkräften und Gewichtskraft und die Summe der Drehmomente Null ergibt. 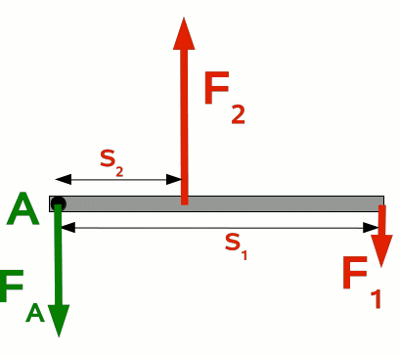
HebelEin an einer Achse befestigter oder aufliegender starrer, stabförmiger Körper wird als Hebel bezeichnet.Auf dem Bild links ist der Hebel am Punkt A drehbar gelagert. Bewegt sich der Hebel aufgrund der an ihm angreifenden Kräfte nicht, so bedeutet das, dass die Summe der auf ihn einwirkenden Drehmomente Null ergibt: F1 * s1 + F2 * s2 = 0 oder F2 = - s1 / s2 * F1 Ist z.B. s1 drei mal so lang wie s2 ergibt sich durch Einsetzen: F2 = -(3 * s2) / s2 * F1 oder F2 = -3 * F1 Mit einem Hebel kann man also kleine Kräfte in große Kräfte "übersetzen". Erkauft wird das mit dem Nachteil, dass die kleine Kraft über eine längere Wegstrecke aufgebracht werden muss, will man mit dem Hebel Lasten bewegen und nicht nur statischen Kräften gegenhalten. Hebel sind Kraftwandler. Zu beachten ist, dass auf den Auflage- oder Drehpunkt des Hebels ebenfalls eine Kraft wirkt. Da sich der Hebel nicht bewegt, muss gelten, dass die Summe der Kräfte Null ergibt: F1 + F2 + FA = 0 oder FA = -(F1 + F2) In dem genannten Beispiel ergibt sich: FA = -(F1 + (-3 * F1)) = 2 * F1 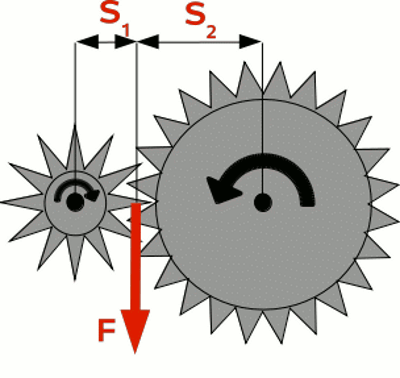
ZahnradgetriebeEin Zahnradgetriebe besteht im einfachsten Fall aus zwei Zahnrädern wie im Bild links zu sehen. In diesem Beispiel besitzt das linke Zahnrad 12 und das rechte Zahnrad 24 Zähne. Der Durchmesser des rechten Zahnrades ist also doppelt so groß wie der des linken Zahnrades. Wird das linke Zahnrad mit dem Drehmoment F * s1 in Rotation versetzt, so greift die Kraft F am rechten Zahnrad mit dem Hebel s2 an. Für das Drehmoment des rechten Zahnrades ergibt sich damit -F * s2. Das Vorzeichen(-) zeigt, dass sich das rechte Zahnrad entgegengesetzt zum linken Zahnrad dreht. Da s2 doppelt so groß wie s1 ist, ergibt sich ein vom Betrag her doppelt so hohes Drehmoment. Die Umdrehungsgeschwindigkeit ist jedoch nur halb so groß wie die des linken Zahnrades. Damit wird von dem rechten Zahnrad die selbe Arbeit verrichtet wie von dem linken. Das Getriebe funktioniert natürlich auch in umgekehrter Richtung. Wird das rechte Zahnrad angetrieben, so dreht sich das linke Zahnrad doppelt so schnell, jedoch nur mit dem halben Drehmoment.Getriebe sind Drehmomentwandler.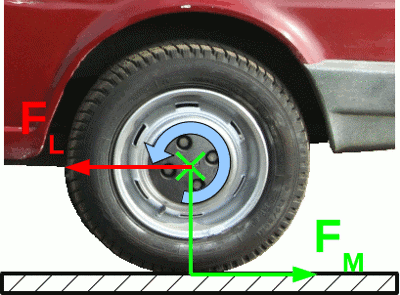
Fortbewegung mit RädernHaben wir bislang bei der Betrachtung von Drehmomenten die Kraftwirkung auf das als ruhend anzusehende Lager nur als Nebeneffekt kennen gelernt, so ist dies beim Radantrieb die gewünschte Vortriebswirkung.Im linken Bild wirkt durch einen Motor ein Drehmoment auf das abgebildete Rad. Dadurch wirkt auf der Radaußenfläche eine entsprechende Kraft FM. Überschreitet diese Kraft nicht die Losbrechkraft (siehe Kapitel "Haftreibung"), so stellt der Auflagepunkt des Rades auf der Straße den Drehpunkt des Systems dar und die Radachse wird mit der gleich großen, aber genau entgegengesetzt wirkenden Kraft Gegenkraft FL nach links gezogen. Die Kraft auf das Radlager treibt also das Fahrzeug an. <<< Arbeit, Energie, Leistung Fahrzeugauslegung >>> Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum |
|
|