|
|
|
|
Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Download Reaktionen Spiele Gadgets Kontakt <<< Fahrzeugauslegung Java-Applet "Tour de Eco" >>> LeistungsbilanzenDie folgenden Funktionsgraphen zeigen die Leistungsbilanzen in verschiedenen Fahrzuständen auf. Berücksichtigt werden die eingesetzte Motorleistung, die in kinetische und potentielle Energie umgesetzte Leistung, sowie die zur Überwindung des Luft- und Rollwiederstandes aufzubringende Leistung. Erstellt wurden die Graphen mit dem Java-App "Tour de Eco" auf der nächsten Seite.Die Versuchsstrecke besteht aus einer 2km langen Geraden ohne Steigung, einer 2km langen 5%igen Steigung, wiederum einer 2km langen flachen Strecke, einem 2km langen 5%igen Gefälle und abschließend einer 2km flachen Strecke. Als Fahrzeugdaten sind die für das Projektfahrzeug mit Originalmotor gültigen Werte verwendet worden (CW=0,47; A=1,51; CR=0,02; m=765kg=Leergewicht + halbe Zuladung; P=17kW). Aufgetragen ist die Leistung (y-Achse) gegen die zurückgelegte Fahrstrecke (x-Achse). Da in dem Java-App der Funktionsplotter permanent von rechts nach links läuft, ist die bislang zurückgelegte Strecke am Ende der x-Achse abzulesen (roter Kringel in Bild 1) und nach links hin sind die Leistungszustände der früheren Streckenabschnitte zu sehen. Beschleunigung aus dem Stand auf gerader Strecke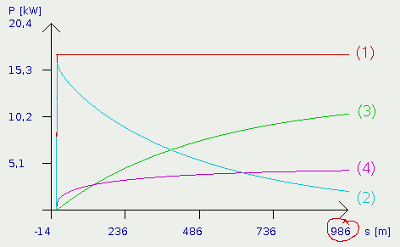
Am Startpunkt wird das virtuelle Gaspedal voll getreten und auf dem Bodenblech gelassen. Entsprechend schnellt der rote Graph (1) von Null auf 17kW. Die damit freigesetzte Motorleistung verpufft nicht wirkungslos im Nirvana, sondern wird in kinetische und in Wärmeenergie umgesetzt. Die Wärmeenergie wird durch die Roll- und Luftreibung hervorgerufen, die mit steigender Geschwindigkeit zunehmen. Anfangs ist unser Auto langsam und somit wird nur ein kleiner Teil der eingesetzten Motorleistung zur Überwindung der Reibung verwendet. Was davon übrig bleibt, wird vollständig in kinetische Energie gesteckt. Somit ist während des Beschleunigungsvorganges auf gerader Strecke zu jedem Zeitpunkt die Summe aus kinetischer, Roll- und Luftwiderstandsleistung gleich der eingesetzten Motorleistung. Mit zunehmender Geschwindigkeit steigt die aufzuwendende Rollwiderstandsleistung linear (Formel [2.5]) und die Luftwiderstandsleistung kubisch (v3, Formel [2.16]). Da hier die Leistung nicht gegen die Fahrzeuggeschwindigkeit, sondern gegen die zurückgelegte Wegstrecke aufgetragen ist, sind die sich ergebenden Zusammenhänge deutlich komplexer, was uns an dieser Stelle aber nicht stören soll. Halten wir einfach mal fest, dass Luft-und Rollreibung mit der Geschwindigkeit anwachsen und somit immer weniger Leistung zum Aufbau von kinetischer Energie verbleibt. Als Konsequenz davon, beschleunigt unser Auto pro zurückgelegter Wegstrecke immer langsamer, aber es gilt an jedem Wegpunkt beim Beschleunigen: PMotor (1) = PKin (2) + PLuft (3) + PRoll (4) Dabei bedeutet:PLuft - Luftwiderstandsleistung, PRoll Rollwiderstandsleistung, PKin - Kinetische Leistung, PMotor - Motorleistung 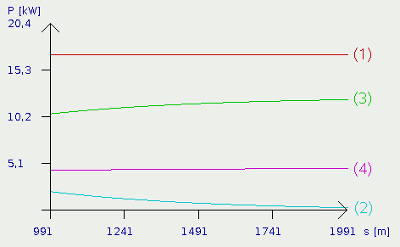
Die Steigungen der Graphen flachen immer mehr ab und die Leistung zum Aufbau weiterer kinetischer Energie (2) tendiert gegen Null, bleibt rein theoretisch aber immer von Null verschieden. Praktisch bedeutet das, dass das Auto irgendwann seine Höchstgeschwindigkeit erreicht. Die Simulation mit Hilfe der Java-App ergibt einen Grenzwert knapp unterhalb von 111km/h. Im Fahrzeugschein des Projektfahrzeugs ist die Höchstgeschwindigkeit mit 105km/h angegeben. Somit stimmen Simulation und Wirklichkeit in erster Näherung recht gut überein. In der Praxis wird kein Motor beständig und bei jeder Drehzahl seine volle Leistung abgeben und außerdem steigt die Motorreibung und somit die Verlustleistung mit der Motordrehzahl an, was hier keine Berücksichtigung findet. Zur Motorcharakteristik werden wir mehr in den Kapiteln zum Elektromotor lernen. Im Gleichgewicht beim Erreichen der Endgeschwindigkeit (PKin=0) gilt: PMotor (1) = PLuft (3) + PRoll (4) Dabei bedeutet:PLuft - Luftwiderstandsleistung, PRoll Rollwiderstandsleistung, PKin - Kinetische Leistung, PMotor - Motorleistung Steigungen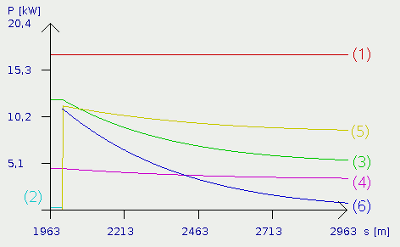
Wie bereits erwähnt, stößt unser Projektauto in der Simulation nach 2km Fahrstrecke auf eine 5%ige Steigung. In dem Rechenmodell ist in der Fahrbahn ein Knick und die Leistungsbilanzen ändern sich entsprechend abrupt. In der Realität sind solche Übergänge immer mehr oder weniger fließend, was auf die Bilanzen an sich aber keinen wesentlichen Einfluss hat. Wer schon einmal ein einem nicht gerade üppig motorisierten Fahrzeug bergauf gefahren ist, wird festgestellt haben, dass sich die Höchstgeschwindigkeit selbst beim Einsatz der vollen Motorleistung auf einem deutlich niedrigeren Niveau einpendelt als beim Fahren in der Ebene. Ursache dafür ist die Tatsache, dass neben den schon angesprochenen Leistungsaufwendungen für den Luft- und Rollwiderstand, sowie die kinetische Energie beim Beschleunigen, auch noch Leistung für den Aufbau von potentieller Energie abgezweigt wird. In dem Funktionsgraphen ist der Beginn der Steigung deutlich zu sehen. Die Kurve für die Luftwiderstandsleistung (3) knickt spontan nach unten ab. Da der Luftwiderstand deutlich von der Fahrzeuggeschwindigkeit abhängt, ist hiermit ersichtlich, dass das Fahrzeug langsamer wird. Weniger ausgeprägt ist dieser Knick in der Rollwiderstandsleistung (4), aber auch hier ist die Abnahme sichtbar. Völlig verschwunden ist die Kurve für die kinetische Leistungsaufwendung (2), die links unten, kurz vor Beginn der Steigung noch zu sehen ist. Kinetische Energie wird nur dann aufgebaut, wenn das Fahrzeug schneller wird. Wie wir bereits gesehen haben, nimmt die Fahrzeuggeschwindigkeit mit Erreichen der Steigung jedoch ab. Jetzt kommt uns der absolut positive Effekt der kinetischen Energie zugute: Im Gegensatz zur Leistung für Roll- und Luftwiderstand, die unserem System verloren gehen, wird die kinetische Energie "gespeichert". Genau wie die kinetische Energie uns am Beschleunigen hindert, hindert sie uns auch am Abbremsen, nur dass die Leistung jetzt nicht der Motorleistung entzogen wird, sondern diese quasi unterstützt! Hinzugekommen ist im Funktionsgraph daher Kurve (6), welche die nun in unser System eingespeiste kinetische Leistung zeigt. Die kinetische Energie steigt wie in Formel [2.12] angegeben, quadratisch mit der Geschwindigkeit, wodurch die Unterstützung der Motorleistung durch den Abbau kinetischer Energie auch um so geringer ausfällt, je langsamer unser Auto wird, d.h, je länger dieses bergauf fährt. Das ist also der Grund, warum Steigungen schneller überwunden werden können, wenn man zuvor "Schwung holt". Ebenfalls neu im Funktionsgraphen ist die Kurve für die potentielle Leistung (5). Wie bereits gesagt, liegt die Ursache für das langsamer werden darin, dass diese potentielle Leistung ebenfalls von der zugeführten Leistung (Motorleistung + kinetische Leistung) abgezweigt wird. Vom Aufbau potentieller Energie spricht man, wenn ein Körper entgegen einem Kraftgefälle angehoben wird. Dass ein Fahrzeug bei Bergauffahrt angehoben wird, dürfte jedem klar sein. Aus Formel [2.11] ist ersichtlich, dass diese potentielle Energie linear mit der Höhe zunimmt. Da wir in der Ebene keinen Höhengewinn oder -verlust zu verzeichnen haben, ist hier die potentielle Leistungsaufwendung schlichtweg Null. Mit Beginn der Steigung ändert sich das aber schlagartig und die entsprechende Kurve schnellt nach oben. Der Höhengewinn pro Zeit (=Leistung) ist bei konstanter Steigung abhängig von der Fahrzeuggeschwindigkeit. Da diese abnimmt, sinkt auch die von der Motorleistung abgezweigte Leistung für den Aufbau potentieller Energie, was an dem Kurvenverlauf zu sehen ist. Das Gesamtsystem strebt auch hier einem Gleichgewichtszustand entgegen, woraus eine Maximalgeschwindigkeit für die entsprechende Steigung resultiert. Mit den angegebenen Simulationswerten liegt diese bei circa 82 km/h. An Steigungen gilt beim "langsamer werden": PLuft (3) + PRoll (4) + PPot (5) = PMotor (1) + PKin (6) Im Gleichgewicht (PKin=0):PLuft (3) + PRoll (4) + PPot (5) = PMotor (1) Beim Beschleunigen:PLuft (3) + PRoll (4) + PPot (5) + PKin (3) = PMotor (1) Dabei bedeutet:PLuft - Luftwiderstandsleistung, PRoll Rollwiderstandsleistung, PPot - Potentielle Leistung, PMotor - Motorleistung Auf dem Plateau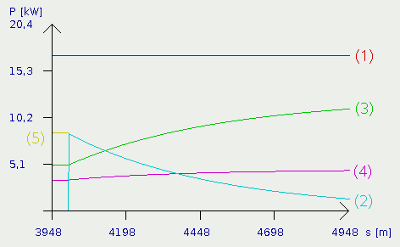
Nach der 5%igen Steigung folgt wieder ein ebenes Teilstück. Das Ende der Steigung ist wiederum deutlich im Funktionsgraphen auszumachen. Kurve (5) mit der potentiellen Leistung verschwindet (wird Null), Luft- und Rollwiderstandsleistung beginnen zu steigen und es wird wieder kinetische Energie aufgebaut (2). Es gelten die gleichen Zusammenhänge wie bereits weiter oben im Kapitel über die Beschleunigung in der Ebene besprochen. Das Auto beschleunigt lediglich nicht aus dem Stand, sondern mit der Endgeschwindigkeit für die Bergaufpassage als Anfangswert. Gefälle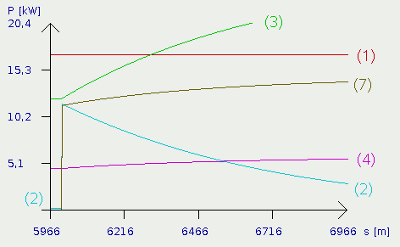
Wir haben bereits gesehen, dass die kinetische Energie unserem Fahrzeug erhalten bleibt. Ebenso verhält es sich mit der potentiellen Energie. Während der Aufbau dieser "Höhenenergie" von der Motorleistung abgezweigt wurde, wird diese in Gefällstrecken der Motorleistung zugeführt. In dem Funktionsgraphen ist klar abzulesen, dass unser Fahrzeug wieder zu beschleunigen beginnt. Die Kurve für die kinetische Leistung (2) schnellt nach oben, Roll- und Luftwiderstandsleistung steigen deutlich. Der Grund ist im Auftauchen von Kurve (7) zu sehen, welche den Verlauf der zugeführten potentiellen Leistung anzeigt. Im Gegensatz zur zugeführten kinetischen Leistung in der Bergaufpassage, steigt die zugeführte potentielle Leistung mit Zunahme der Geschwindigkeit sogar noch an! Da unser Auto immer schneller wird, sinkt es bei gleichbleibendem Gefälle auch immer schneller und somit wird halt auch beständig mehr potentielle Leistung zugeführt. Das geht sogar so weit, dass alleine die Leistung zur Überwindung des Luftwiderstandes (3) irgendwann größer ist als die Motorleistung! Sie "verschwindet" sogar am oberen Ende des Koordinatensystems. Mit den Simulationsparametern ergibt sich auf der Gefällstrecke eine Endgeschwindigkeit von immerhin fast 140km/h! An Gefällstrecken gilt beim Beschleunigen: PLuft (3) + PRoll (4) + PKin (2) = PMotor (1) + PPot (7) Im Gleichgewicht (PKin=0):PLuft (3) + PRoll (4) = PMotor (1) + PPot (7) Beim langsamer werden:PLuft (3) + PRoll (4) = PMotor (1) + PPot (7) + PKin (6) Dabei bedeutet:PLuft - Luftwiderstandsleistung, PRoll Rollwiderstandsleistung, PPot - Potentielle Leistung, PMotor - Motorleistung Wieder auf Ausgangshöhe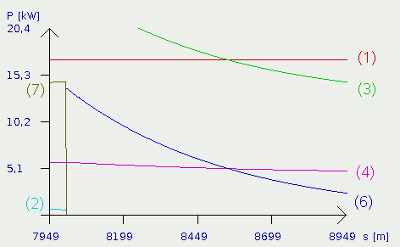
Bei Fahrkilometer 8 ist die Gefällstrecke zu ende und das ist ebenfalls deutlich am Funktionsgraphen zu sehen. Die potentielle Leistungszufuhr verschwindet (7) und steht somit nicht mehr als zusätzliche Eingangsleistung zur Verfügung. Entsprechend wird das Fahrzeug wieder langsamer und kinetische Energie wird dem Fahrzeug entzogen. Kurve (6) zeigt die abfallende kinetische Leistungszufuhr an. Wie immer wenn das Fahrzeug langsamer wird, sinken Luft- und Rollwiderstandsleistung (3) + (4). Das System strebt wieder dem Gleichgewichtszustand mit der Endgeschwindigkeit in der Ebene (111km/h) zu. Im Gegensatz zur Beschleunigung aus dem Stand, ist die Geschwindigkeit immer zumindest etwas höher. Beim langsamer werden in der Ebene gilt: PLuft (3) + PRoll (4) = PMotor (1) + PKin (6) Dabei bedeutet:PLuft - Luftwiderstandsleistung, PRoll Rollwiderstandsleistung, PMotor - Motorleistung Bremsen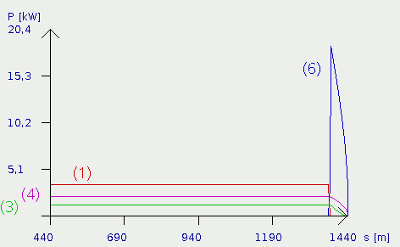
Weiter oben haben wir gesehen, dass kinetische Energie beim Erklimmen von Steigungen recht hilfreich sein kann. Der negative Aspekt macht sich beim Bremsen bemerkbar. Bremsen bedeutet wie Beschleunigen, dass die Geschwindigkeit eines Fahrzeuges geändert wird. Spricht man bei Fahrzeugen von Beschleunigen, so meint man damit, dass der Betrag (der Wert) der Geschwindigkeit in Bezug auf die Erdoberfläche erhöht wird. Umgekehrt spricht man von Bremsen, wenn der Geschwindigkeitsbetrag in Relation zur Erdoberfläche verringert wird. In beiden Fällen wird Arbeit verrichtet und somit Leistung benötigt. In der nebenstehenden Abbildung ist der Bremsvorgang aus einer Geschwindigkeit von ca. 15m/s (52km/h) auf 0m/s mit konstanter Verzögerung zu sehen. Die kinetische Leistung, welche dem Verzögerungsvorgang entgegenwirkt, springt mit Beginn des Bremsvorganges auf ihren Maximalwert, der sogar über der Motorleistung liegt und fällt zunehmend schneller auf den Wert Null. Wie aus Formel [2.12] zu ersehen, wird in dem genannten Beispiel kinetische Energie in Höhe von SchlussfolgerungDie Knackpunkte auf Seiten der Fahrzeugmechanik liegen offen und wir können berechnen, welche Energiemenge wir für unterschiedliche Fahrsituationen benötigen. Die Rechnungen mit den für das Projektfahrzeug geltenden Werten haben gezeigt, dass auf mechanischer Seite durchaus Optimierungsbedarf in Sachen Luftwiderstandsbeiwert und Rollwiderstand bestehen. Dass auch Gewichtsreduzierung vorteilhaft ist, wird sich noch zeigen, wenn es an die Dimensionierung der Fahrakkus geht.Auf der nächsten Seite findet ihr einen "Fahrsimulator" der euch zeigt, welche Energiemenge ihr beim Durchfahren eines gegebenen Streckenprofils benötigt. Kleine Bemerkung zum Anlegen eigener Teststrecken in der Java-Applikation: Die Strecke wird aus bis zu 100 Teilstrecken zusammengesetzt. Die Teilstrecken sind durchnummeriert () und auf die Nummer folgt nach dem Gleichheitszeichen als erstes die Angabe der Länge der Teilstrecke von 1 bis 10000m und nach dem Schrägstrich folgt die Angabe der Steigung von -20 bis 20. Jeder Abschnitt muss durch ein Semikolon (;) abgeschlossen werden ! Die Streckenführung wird bis zum ersten Teilstück mit der Länge 0m eingelesen und eine eventuell auftretende Höhendifferenz wird durch Einfügen eines weiteren Teilstückes mit 20% Steigung bzw. -20% Gefälle ausgeglichen. Wer kann schon ein Leben lang bergab fahren... Es ist nicht möglich, die Strecke zu speichern! Wenn ihr das Programm beendet und neu startet, werden wieder die Standardwerte übernommen. Ihr könnt aber per "Copy & Paste" Daten aus jedem Textprogramm übernehmen bzw. an die Java-App übergeben. Beispiele einfacher Strecken: Gerade Strecke: (1) = 10000 / 0; Berg und Hügel mit 15% Steigung / Gefälle: (1) = 100 / 0; (2) = 2000 / 15; (3) = 10 / 0; (4) = 2000 / -15; (5) = 100 / 0; (6) = 300 / 15; (7) = 10 / 0; (8) = 300 / -15; (9) = 100 / 0; Buckelpiste: (1) = 100 / 0; (2) = 10 / 5; (3) = 10 / 10; (4) = 10 / 15; (5) = 10 / 10; (6) = 10 / 5; (7) = 10 / 0; (8) = 10 / -5; (9) = 10 / -10; (10) = 10 / -15; (11) = 10 / -10; (12) = 10 / -5; (13) = 100 / 0; Spielt einfach ein wenig mit den Werten und testet aus, wie viel Energie ihr zum Durchfahren eines Streckenprofils mit unterschiedlichen Geschwindigkeiten, unterschiedlich schweren und motorisierten Fahrzeugen benötigt. In der Applikation ist dazu ein Stromzähler eingebaut, der euch verrät, wie ökonomisch ihr euch mit eurem Auto fortbewegen könnt. <<< Fahrzeugauslegung Java-Applet "Tour de Eco" >>> Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum |
|
|