|
|
|
|
Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Download Reaktionen Spiele Gadgets Kontakt <<< Energie von Magnetfeldern Gleichstrommotor (permanenterregt) >>> Elektrische SchwingkreiseMechanisches PendelAls Schwingung bezeichnet man die periodische Umwandlung zweier Energieformen. Betrachten wir die dabei ablaufenden Vorgänge in einem mechanischen System: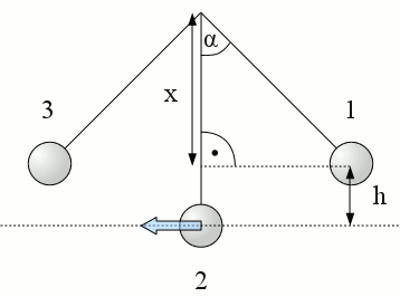
Mechanisches Pendel: Die Anordnung besteht aus einer Eisenkugel der Masse m, die an einem dünnen Faden der Länge l aufgehängt ist. In Position (2) befindet sich die Anordnung in ihrer Ruhelage. Nun lenken wir die Kugel um einen Winkel α aus. Dabei wird die Kugel um die Höhe h angehoben, womit dem System potentielle Energie zugeführt wird. Die potentielle Energie errechnet sich zu: Die Höhe h errechnet sich dabei aus der Fadenlänge und dem Winkel zu: Nun lassen wir die Kugel los. Diese beginnt sofort im Schwerefeld der Erde nach unten zu fallen und wird durch den Faden auf eine Kreisbahn nach links gelenkt. Die potentielle Energie wird dabei in Bewegungsenergie umgewandelt (die Kugel wird beschleunigt). Im Punkt (2) ist die zugeführte potentielle Energie vollständig in Bewegungsenergie umgewandelt worden. Dabei gilt: Die in der Kugel steckende kinetische Energie bewirkt, dass diese sich weiter nach links bewegt. Dabei wird die Kugel nun auf ihrer Kreisbahn angehoben, baut damit potentielle Energie auf und wird langsamer. Zum Stillstand kommt sie im Punkt (3). Ohne Berücksichtigung von Reibung (Luftreibung, verbiegen des Fadens) hat die Kugel dabei die gleiche Höhe erreicht wie zu Beginn der Bewegung. Der Auslenkwinkel ist vom Betrag her gleich groß wie zu Beginn der Bewegung, zeigt allerdings in die entgegengesetzte Richtung. Die potentielle Energie wird bis zum Punkt (2) erneut vollständig in kinetische Energie verwandelt, wobei die Fallbewegung aufgrund des Fadens nach rechts geleitet wird. Von Punkt (2) zu Punkt (1) wird die kinetische Energie wieder vollständig in potentielle Energie umgesetzt. Wieder an Punkt (1) angelangt ist eine vollständige Periode durchlaufen und der Prozess beginnt erneut. Berücksichtigen wir die Reibung, so wird dem System laufend Energie in Form von Wärme entzogen. Die Auslenkung an den Wendepunkten (1) + (3) bzw. die Geschwindigkeit im Punkt (2) wird zunehmend geringer, bis das Pendel schließlich in Punkt (2) zur Ruhe kommt. Energiewandlung in elektrischen SchwingkreisenBetrachten wir einen elektrischen Stromkreis bestehend aus einer Spule und einem Kondensator. Wie bei dem mechanischen Pendel passiert hier nichts, so lange dem System keine Energie zugeführt wird. Das machen wir gedanklich, indem wir den Kondensator auf die Spannung U0 aufladen. Damit liegt die Kondensatorspannung gleichzeitig an der Spule an. Wie wir im Kapitel zu Schaltvorgängen und zur Selbstinduktion gesehen haben, baut die Spule eine Spannung auf, die dem Stromfluss durch die Spule entgegenwirkt. Es fließt zunächst ein kleiner Strom, der stark, dann schwächer ansteigt. Dabei wird der Kondensator entladen und die Feldstärke zwischen den Platten nimmt ab. In der Spule baut sich im Gegenzug ein immer stärker werdendes Magnetfeld auf. Die Energie wird nach und nach von dem elektrischen Feld des Kondensators zu dem Magnetfeld der Spule transferiert. Sobald der Kondensator entladen ist, fließt der maximale Strom durch den Stromkreis und die gesamte Energie steckt nun in dem Magnetfeld der Spule. Ohne antreibende Spannung nimmt die Stromstärke durch die Spule ab diesem Zeitpunkt ab. Der Lenz'schen Regel folgend baut sich dadurch in der Spule eine Induktionsspannung auf, die den Stromfluss zu erhalten sucht. Dadurch wird der Kondensator erneut aufgeladen, allerdings mit entgegengesetzter Polung. Die Induktionsspannung der Spule sinkt auf Null, sobald das Magnetfeld vollständig abgebaut ist. Die gesamte Energie steckt erneut in dem elektrischen Feld des Kondensators. Der Entladevorgang des Kondensators läuft erneut ab, der Strom fließt dabei jedoch in die Gegenrichtung. Wieder baut sich ein Magnetfeld in der Spule auf, dessen Feldlinien nun um 180 Grad gedreht verlaufen. Ist der Kondensator entladen, lädt die Spule den Kondensator erneut auf. Die Polung ist jetzt wie zu Beginn des Versuchs. Eine vollständige Schwingung ist durchlaufen und die Prozesse beginnen von vorne. Vernachlässigt man den ohmschen Widerstand, so laufen diese Prozesse endlos ab.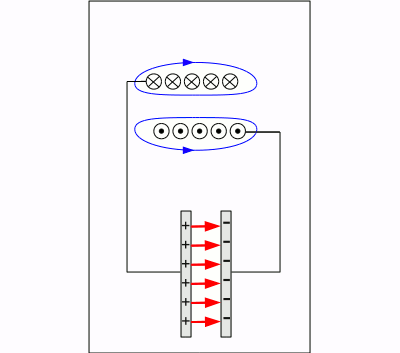
Elektrischer Schwingkreis aus eine Spule und einem Kondensator: Frequenz elektrischer SchwingkreiseDie Frequenz eines verlustfreien Schwingkreises aus einem Kondensator und einer Spule ergibt sich zu: Dabei bedeutet:f0 - Frequenz, L - Induktivität der Spule, C - Kapazität des Kondensators Kondensatoren und Spulen arbeiten allerdings keinesfalls verlustfrei. Die größte "Bremse" für den elektrischen Strom ist dabei der Widerstand des Spulendrahtes. Diesen kann man sich als in Reihe zur Spule geschaltet vorstellen. 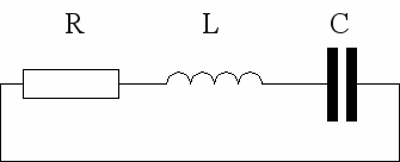
Elektrischer Schwingkreis bestehend aus einem ohmschen Widerstand (R), einer Spule (L) und einem Kondensator (C). Daher wird eine derartige Anordnung auch als RLC Kreis bezeichnet. Der Widerstand wandelt beständig einen Teil der in dem Schwingkreis befindlichen Energie in Wärmeenergie, die dem System entzogen wird. Die Maximalspannung des Kondensators bzw. der Maximalstrom durch die Spule werden dadurch immer geringer, bis schließlich die gesamte Energie in Wärmeenergie verwandelt worden ist. Für die Resonanzfrequenz einer derartigen Schaltung gilt: Dabei bedeutet: fr - Resonanzfrequenz, L - Induktivität, C - Kapazität, R - Widerstand Die Resonanzfrequenz bezeichnet die Frequenz, bei der der Widerstand der Schaltung beim Anliegen einer (meist sinusförmigen) Wechselspannung ihren niedrigsten Wert erreicht. <<< Energie von Magnetfeldern Gleichstrommotor (permanenterregt) >>> Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum |
|
|