|
|
|
|
Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Download Reaktionen Spiele Gadgets Kontakt <<< Magnetismus Magnetische Permeabilität >>> SpulenMagnetfeld einer punktförmigen Ladung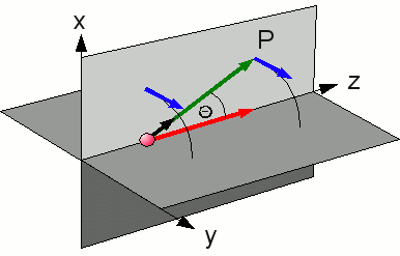
Die Feldlinien einer gleichförmig bewegten Punktladung verlaufen ringförmig um die Bewegungsachse. Auf dem Bild bewegt sich die positive Punktladung auf der z-Achse nach rechts. Beim Blick in Bewegungsrichtung der Ladung verlaufen die Feldlinien im Uhrzeigersinn. Die dunkelblauen Pfeile zeigen die Vektoren der magnetischen Flussdichte und der rote Pfeil den Geschwindigkeitsvektor. Für die magnetische Flussdichte im Abstand r gilt: Dabei bedeutet: B - Magnetische Flussdichte, μ - magnetische Leitfähigkeit, q - Ladung, v - Geschwindigkeit, r - Abstand, n - Einheitsvektor von der Punktladung zum Punkt P Für den Betrag der magnetischen Flussdichte im Abstand r ergibt sich damit: Dabei bedeutet: B - Magnetische Flussdichte, μ - magnetische Leitfähigkeit, q - Ladung, v - Geschwindigkeit, r - Abstand, Θ - Winkel zwischen v und dem Abstandsvektor zum Punkt P Magnetfeld eines geraden LeitersWie bereits erwähnt, bewegen sich Elektronen durch einen stromdurchflossenen elektrischen Leiter. Das Magnetfeld dieser Elektronen addiert sich zu dem Gesamtfeld des Leiters. Für einen geraden, unendlich langen Leiter ergibt sich für den Betrag des magnetischen Flusses im Abstand r:Dabei bedeutet: B - Magnetische Flussdichte, μ - magnetische Leitfähigkeit, I - Stromstärke, r - Abstand Diese Formel ist auch auf den mittleren Bereich endlich ausgedehnter Leiter gut anwendbar, sofern der Abstand r im Vergleich zur Leiterlänge klein gewählt wird. An den Leiterenden und in großem Abstand ist die Geometrie des Magnetfeldes nicht mit dem Idealbild des unendlich ausgedehnten Leiters vergleichbar. Überlagerung von MagnetfeldernWie auf der vorhergehenden Seite gesehen, können sich Magnetfelder derart überlagern, dass sich die Stärke des resultierenden Feldes (zumindest lokal) erhöht oder erniedrigt. Wird das Magnetfeld von einem stromdurchflossenen Leiter erzeugt, so müssen zur Verstärkung des Magnetfeldes zwei oder mehr nebeneinander liegende Drähte in der selben Richtung von Strom durchflossen werden. Eine derartige Anordnung von Drähten erhält man am einfachsten, indem man einen langen Draht auf einem Rohr oder Stab aufwickelt. Das Resultat sind viele dicht beieinander liegende Drahtwindungen, die beim Anliegen einer Spannung alle in der selben Richtung von Strom durchflossen werden. Somit wird das resultierende Magnetfeld vielfach verstärkt.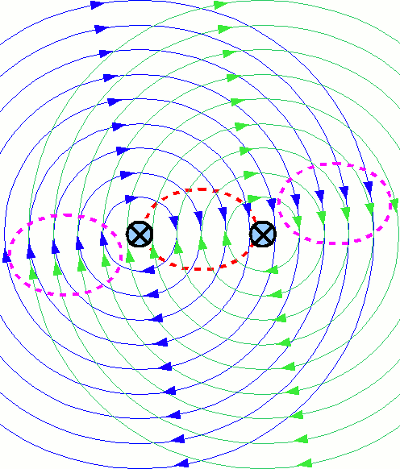
Magnetfeldlinien zweier stromdurchflossener Drähte: Der Blick geht von oben auf die beiden im Querschnitt abgebildeten Drähte. Der Strom fließt dabei in die Bildschirmebene hinein. Dargestellt wird diese Richtung durch ein Kreuz in dem Draht, was einen von hinten zu sehenden Pfeil symbolisiert. Daraus ergibt sich ein Magnetfeld mit im Uhrzeigersinn verlaufenden Magnetfeldlinien. Die Feldlinien des linken Drahtes sind in blau, die des rechten Drahtes in grün gezeichnet. So wie auf dem Bild verlaufen die Feldlinien allerdings nur, wenn nur durch je einen der beiden Drähte ein Strom fließt. Wenn beide Drähte gleichzeitig von Strom durchflossen werden, überlagern sich die beiden Felder zu einem gemeinsamen Magnetfeld. Wie zu sehen, laufen die Feldlinien der (ungestörten) Felder in dem rot markierten Bereich entgegengesetzt, was bedeutet, dass die Feldlinien dort heraus gedrängt werden,in den pink markierten Bereichen dagegen gleichsinnig, was einer Verstärkung des Magnetfeldes an diesen Stellen gleichkommt. 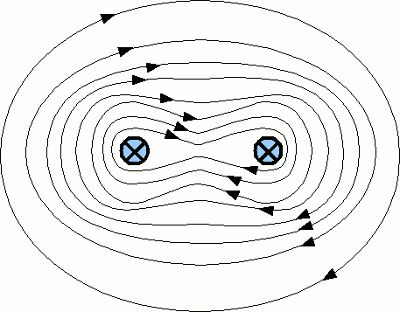
Das sich aus der Überlagerung der beiden obigen Magnetfelder ergebende Feld ist hier zu sehen. Die Feldlinien werden aus dem Zwischenraum heraus gedrängt und mit zunehmendem Abstand werden die Feldlinien von knochenförmig zu oval und schließlich rund. In Großem Abstand zu den beiden Drähten ähnelt das Feldlinienbild dem eines einzelnen stromdurchflossenen Leiters mit der doppelten Stromstärke. Das Magnetfeld wird im Zwischenraum der Drähte geschwächt und außerhalb verstärkt, wodurch eine Kraftwirkung entsteht, welche die beiden Drähte anzieht. 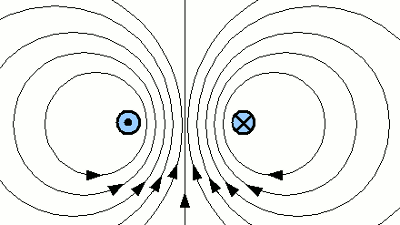
Fließt der Strom in entgegengesetzter Richtung durch die beiden Drähte (linker Draht aus der Bildschirmebene, rechter Draht hinein), wird das Magnetfeld im Zwischenraum der Drähte verstärkt und außerhalb geschwächt. Das Resultat ist eine Abstoßende Kraftwirkung zwischen den beiden Drähten. 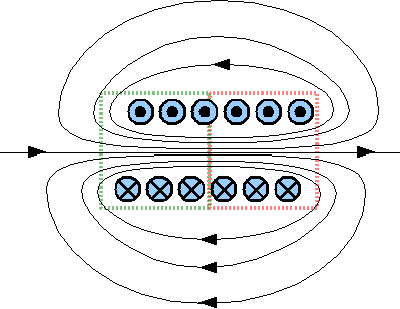
In diesem Bild ist ein Querschnitt durch eine Spule mit 6 Drahtwindungen gezeichnet. Der Strom fließt in der unteren Bildhälfte in die Bildschirmebene hinein (Kreuz, von hinten betrachteter Pfeil) und in der oberen Bildhälfte aus dem Bildschirm heraus (Punkt, Pfeilspitze von vorne). Die resultierenden Magnetfeldlinien der unteren Bildhälfte verlaufen somit im Uhrzeigersinn, in der oberen hingegen entgegen dem Uhrzeigersinn. Weiterhin treten die Feldlinien in der rechten Bildhälfte aus der Spule heraus und auf der linken Bildhälfte wieder ins Spuleninnere ein. Das Feldlinienbild ähnelt stark dem eines Stabmagneten mit dem Südpol auf der linken Spulenseite (grünes Rechteck) und dem Nordpol auf der rechten Seite (rotes Rechteck). Wie bereits erwähnt, wirken Kräfte zwischen stromdurchflossenen Drähten. In der hier abgebildeten Spule werden die Drahtwindungen von links und rechts aneinander gepresst, im Spuleninnern wirkt jedoch ein "Überdruck", der die Spule radial nach außen drückt. Bei Spulen mit sehr hohen Strömen und daraus resultierenden starken Magnetfeldern (Teilchenbeschleuniger) sind diese Kräfte keineswegs zu vernachlässigen! Das Magnetfeld einer Spule wird durch die Überlagerung der Felder der Drahtwicklungen im Spuleninnern verstärkt. Die Feldlinien verlaufen hier annähernd parallel, was bedeutet, dass das Magnetfeld in diesem Bereich homogen ist. Im Innern einer im Vergleich zum Durchmesser langen Spule mit n Windungen gilt für die Flussdichte: Dabei bedeutet: B - Magnetische Flussdichte, μ - magnetische Leitfähigkeit, I - Stromstärke, n - Anzahl Windungen, l - Länge der Spule Biot-Savart-GesetzDas magnetische Feld, das von einem konstanten elektrischen Strom hervorgerufen wird, kann mit Hilfe des Gesetzes von Biot-Savart berechnet werden:Dabei bedeutet: B - Magnetische Flussdichte, dV - Volumenelement, J - Stromdichte im Volumen dV, μ0 - magnetische Permeabilität, r - Abstandsvektor von dV zu dem Punkt, an dem das Feld berechnet wird Das Gesetz vereinfacht sich unter der Annahme, dass der Strom als durch einen unendlich dünnen Leiter fließend betrachtet werden kann: Dabei bedeutet: B - Magnetische Flussdichte, dV - Volumenelement, I - Strom durch den Leiter, μ0 - magnetische Permeabilität, r - Abstandsvektor von dV zu dem Punkt, an dem das Feld berechnet wird 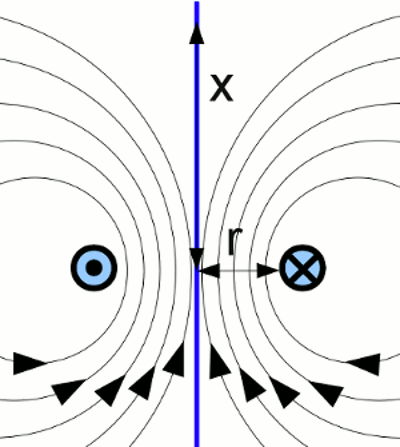
Mit Hilfe dieses Gesetzes erhalten wir für die Flussdichte einer einzelnen Leiterschleife: Dabei bedeutet: B - Magnetische Flussdichte, dV - Volumenelement, I - Strom durch den Leiter, μ0 - magnetische Permeabilität, r - Radius der Leiterschleife, x - Abstand vom Zentrum der Leiterschleife zu einem Punkt auf der Mittelachse Die magnetischen Flussdichten von Formel [3.20] und [3.21] (siehe oben) können ebenfalls aus dem Gesetz von Biot-Savart hergeleitet werden. <<< Magnetismus Magnetische Permeabilität >>> Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum |
|
|