Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Download Reaktionen Spiele Gadgets Kontakt

<<< Logikgatter Relais >>>

Computer

Das Video zum Kapitel

Dualsystem

Das Dualsystem ist der elektronischen Datenverarbeitung weit verbreitet. Die auch als Zweiersystem oder Binärsystem bezeichnete Zahlendarstellung verwendet nur zwei Symbole: 0 und 1. Im Gegensatz dazu verwendet das Dezimalsystem zehn Symbole: 0, 1, 2, 3, 4, 5, 6, 7, 8, und 9. Beim Zählen wird die niederwertigste Stelle, also die am weitesten rechts stehende Ziffer um eins erhöht. Erreicht die niederwertigste Stelle im Dezimalsystem den Wert 9, so wird die nächst höherwertige Stelle, welche sich eine Position weiter links befindet, um 1 erhöht und die Zählung startet an der niederwertigsten Stelle wieder bei 0. Für die dezimale Zählweise erhalten wir:

001, 002, 003, ... 008, 009, 010,
011, 012, 013, ... 018, 019, 020,
...
091, 092, 093, ... 098, 099, 100,
101, 102, 103, ... 198, 199, 200.

Abbildung 1:
Das Zählen im Dualsystem folgt exakt den gleichen Regeln mit Ausnahme der Tatsache, dass nur zwei Symbole verfügbar sind, weshalb die Zählung an der aktuellen Stelle erneut bei 0 beginnt und die nächsthöhere Stelle um eins erhöht wird, sobald eine Stelle den Wert 1 erreicht hat.

Jede Stelle einer Dualzahl entspricht einer Zweierpotenz, wobei die ganz rechts stehende Stelle 2⁰, sie nächsthöhere 2¹, 2² und so weiter entspricht. Die am weitesten rechts stehende Ziffer wird auch als Least Significant Bit, LSB (engl. für am wenigsten bedeutende Einheit), die am weitesten links stehende Stelle als Most Significant Bit, MSB (engl. für höchstwertige Einheit) bezeichnet. In der Computersprache wird eine binäre Stelle, im Englischen binary digit kurz als Bit bezeichnet und es handelt sich hierbei um die kleinstmögliche Informationseinheit. Ein Byte wiederum besteht in der Computerlogik üblicherweise aus acht Bit. Damit kann ein Byte 2⁸ = 256 unterschiedliche Dualzahlen darstellen, welche üblicherweise die Zahlen 0 bis 255 repräsentieren.:

Abbildung 2: (Animation Starten)

Datenspeicherung

Ein Bit kann in einen elektronischen Schaltkreis durch ein Bauteil wie ein bistabiles Kippglied integriert werden, das zwei unterschiedliche Zustände einnehmen kann. Neben diskreten Bauteilen kann ein bistabiles Kippglied auch durch zwei über Kreuz miteinander gekoppelte NOR-Gatter erstellt werden: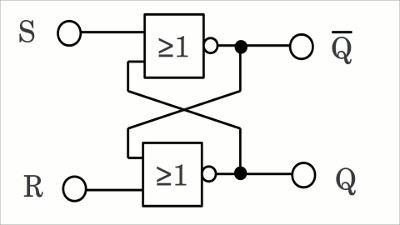

Abbildung 3:
NOR RS Flipflop (englisch: SR NOR latch).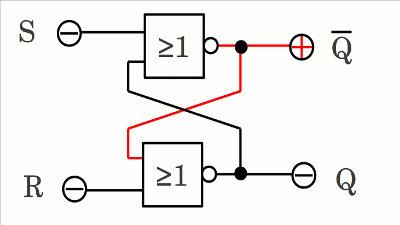

Abbildung 4:
Wann immer der Schaltkreis mit einer Spannungsversorgung verbunden wird, hängt der Anfangszustand von den elektrischen Eigenschaften der verwendeten Bauteile ab. Das Ausgangssignal an Q kann entweder HIGH oder LOW sein. Nehmen wir an, dieses sei auf LOW. Die Eingangssignale an R und S sind ebenfalls auf LOW. Beide Eingänge des oberen NOR-Gatters sind damit auf LOW, womit sich als Ausgangssignal ein HIGH-Pegel ergibt. Der Ausgang des oberen Gatters ist mit einem der Eingänge des unteren Gatters verbunden, womit einer dessen Eingänge auf HIGH und somit der Ausgang auf LOW ist. Der Zustand des Schaltkreises ist stabil. Q ist auf HIGH, und bringt damit das über Kreuz gekoppelte Gatter von Q auf LOW-Pegel, was wiederum das obere Gatter von Q auf HIGH-Pegel hält.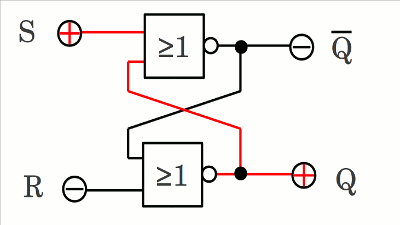

Abbildung 5:
Wird Eingang S auf HIGH-Pegel gebracht, so ändert sich der Zustand des Schaltkreises:
Der Ausgang des oberen Gatters wechselt von HIGH- auf LOW-Pegel, wodurch sich beide Eingänge des unteren NOR-Gatters auf LOW-Pegel befinden. Der Ausgang des unteren Gatters kippt dadurch auf HIGH-Pegel, wodurch sich beide Eingänge des oberen Gatters auf HIGH-Pegel befinden. Der Schaltzustand ist stabil. Q ist HIGH, während Q LOW ist.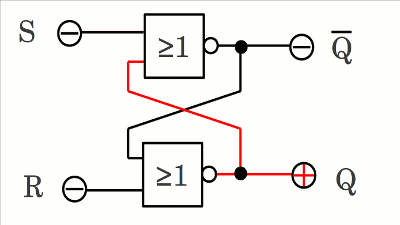

Abbildung 6:
Fällt Eingang S zurück auf LOW-Pegel, so bleibt der Schaltzustand der Ausgänge durch die Rückkopplung über Kreuz erhalten. Während beide Eingänge auf LOW-Pegel sind, befindet sich der Schaltkreis im Erhaltungszustand (engl. hold state).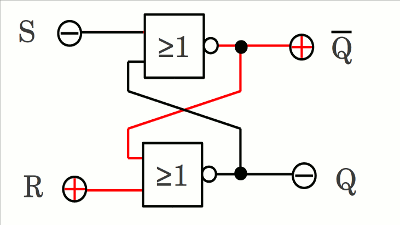

Abbildung 7:
Wird Eingang R auf HIGH-Pegel gebracht und Eingang S gleichzeitig auf LOW-Pegel belassen, so wechselt Q von HIGH auf LOW und zwingt den Ausgang des oberen Gatters durch die Rückkopplung an den Eingang gleichzeitig zum Wechsel von LOW auf HIGH.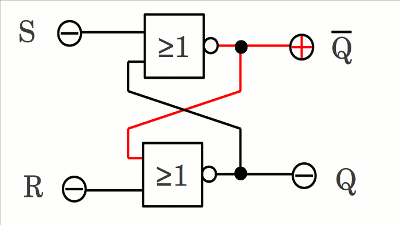

Abbildung 8:
Während des "hold state" behält Q seinen Schaltzustand bei.
Eingang S wird mit Set (Setzen) bezeichnet, da dieser den Ausgang Q auf HIGH-Pegel bringt, während Eingang R mit Reset (Rücksetzen) benannt wird, da dieser den Ausgang Q auf LOW-Pegel zwingt.
Ausgang Q verhält sich komplementär zu Q (Q = NOT Q).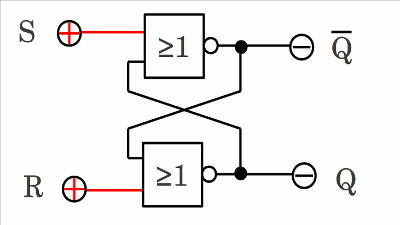

Abbildung 9:
Der Zustand, in dem sich BEIDE Eingänge auf HIGH-Pegel befinden, bezeichnet man als verbotenen Zustand (engl. forbidden state oder restricted combination). In diesem Zustand, der auch als dritter Zustand bezeichnet wird, sind beide Ausgänge Q und Q auf LOW-Pegel und die logische Gleichung Q = NOT Q ist nicht erfüllt. Im normalen Betrieb einer Speicherzelle darf dieser Zustand nicht eintreten.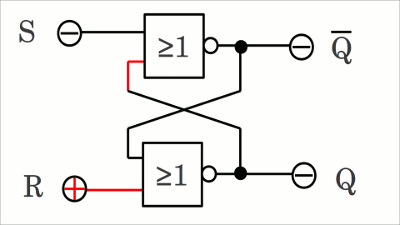

Abbildung 10: (Animation Starten)
Animierte Darstellung eines NOR RS Flipflops (englisch: NOR SR Latch).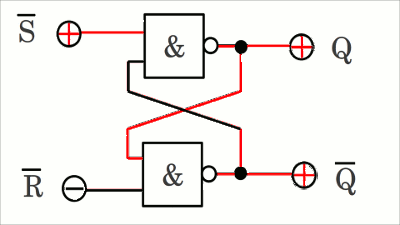

Abbildung 11: (Animation Starten)
Animierte Darstellung eines NAND SR Latch.
Werden zwei über Kreuz gekoppelte NAND-Gatter verwendet, so erfolgt die Steuerung von Set und Reset über LOW-Pegel (active LOW), was durch S beziehungsweise R gekennzeichnet wird.
S = LOW, R = HIGH setzt Ausgang Q auf HIGH-Pegel.
S = HIGH, R = LOW setzt den Ausgang auf LOW-Pegel.
S = HIGH, R = HIGH ist der Erhaltungszustand (hold state).
S = LOW, R = LOW ist der verbotene Zustand (restricted combination).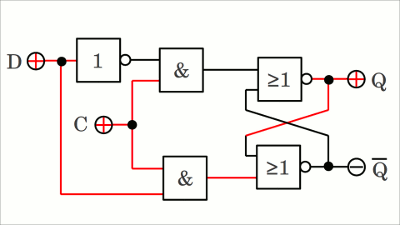

Animierte Zeichnung Taktzustandsgesteuertes RS Flipflop

Abbildung 12: (Animation Starten)
Durch Einfügen weiterer Logikgatter an den Eingängen des RS Flipflops entsteht ein sogenanntes getaktetes oder auch taktzustandsgesteuertes RS Flipflop (englische Bezeichnung gated latch).
Ist Eingang C (Control, Clock) auf LOW-Pegel, so sind die Ausgänge der beiden UND-Gater ebenfalls auf LOW, womit sich die Eingänge des nachgeschalteten RS Flipflops im "hold state" befinden. Kippt C auf HIGH-Pegel, so wird das Gate (englisch für TOR) durchlässig (transparent) und der Zustand des D- (Data) Eingangs wird auf den Ausgang Q übertragen. Der Ausgang wird auf HIGH gesetzt, wenn auch D auf HIGH-Pegel ist und umgekehrt. Eingang C wird bisweilen mit dem Buchstaben E (Enable) bezeichnet.
Die Konfiguration des gated D-latch verhindert das Anlegen des verbotenen Zustands an den Eingängen des bistabilen Kippgliedes.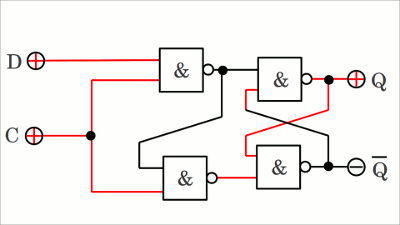

Abbildung 13: (Animation Starten)
Durch Erweitern des Schaltkreises um zwei weitere NAND-Gatter kann ein NAND RS Flipflop in ein taktzustandsgesteuertes RS Flipflop verwandelt werden. Die NAND-Gatter am Eingang invertieren die Eingangssignale, womit ein LOW-Pegel am C-Eingang den Erhaltungszustand an den Eingängen des RS-Flipflops generiert (HIGH-Pegel an beiden Eingängen).
Verursacht durch die Gatterlaufzeiten, kann in der Animation für kurze Zeit der verbotene Zustand (LOW-Signal an beiden Eingängen des RS-Flipflops) beobachtet werden. Weiterhin befinden sich die Ausgänge Q und Q kurzfristig auf gleichem Potential. Auch wenn die Zeichnung die Vorgänge in einem getakteten Flipflop nicht exakt wiedergibt, solltet ihr im Hinterkopf behalten, dass die Signallaufzeit des gesamten Schaltkreises mit jedem hinzugefügten Logikgatter zunimmt. Wird euer "Computer" mit einer zu hohen Taktrate betrieben, so kann der Inhalt der Speicherzelle zerstört werden. Weiterhin darf die Speicherzelle nicht zu jedem Zeitpunkt ausgelesen werden, um falsche Dateninterpretation zu verhindern.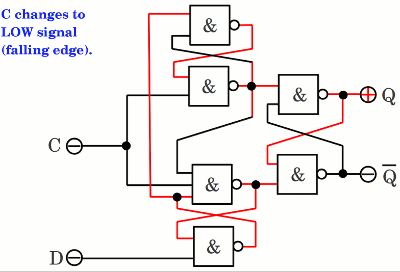

Animierte Zeichnung Vorderflankengesteuertes D-Flipflop

Abbildung 14: (Animation Starten)
Drei NAND RS-Flipflops sind erforderlich, um ein taktflankengesteuertes, genau genommen ein vorderflankengesteuertes D-Flipflop (engl.: positive-edge-triggered D flip-flop) zu kreieren. Wann immer der Clock-Eingang auf LOW-Level ist, befinden sich beide Eingänge des rechten Flipflops am Ausgang auf HIGH-Pegel, unabhängig vom Zustand des Data-Eingangs, womit sich das Flipflop im Erhaltungszustand befindet und den vorherigen Zustand speichert. Abhängig vom Zustand des Data-Eingangs wird Q gesetzt oder zurückgesetzt, wenn der Clock-Eingang von LOW- auf HIGH-Pegel wechselt. Auch wenn der Clock-Eingang auf HIGH-Pegel bleibt, behält Q nun seinen Zustand - selbst bei einem Wechsel des Data-Signals.
Das vorderflankengesteuerte D-Flipflop erfasst den Wert des Data-Eingangs an der steigenden Flanke des Clock-Signals. Abhängig von den Gatterlaufzeiten vergeht einige Zeit, bis das Data-Signal am Ausgang Q anliegt.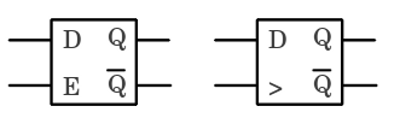

Abbildung 15:
Flipflops sind als integrierte Schaltkreise erhältlich, wobei sich üblicherweise mehrere Flipflops auf einem Chip befinden. Das linke Symbol zeigt ein taktzustandsgesteuertes D-Flipflop (D-Latch), das rechte Symbol ein vorderflankengesteuertes D-Flipflop (positive edge triggered D latch).

Register

Um mehr als nur ein einzelnes Bit speichern zu können, müssen mehrere Flipflops miteinander verschaltet werden. Sind die Flipflops in Serie angeordnet, wobei der Ausgang eines Flipflops mit dem Dateneingang des folgenden Flipflops verschaltet ist und wird ein gemeinsames Clock-Signal verwendet, so bezeichnet man den Schaltkreis als Schieberegister (engl.: shift register). Mit jeder steigenden Flanke des Taktsignals werden alle Bits in der Kette um eine Position verschoben.
Während des Schreibvorgangs wird das jeweilige Daten-Bit des gesamten Bytes am D-Eingang des ersten Flipflops gelesen und mit jedem steigenden Signal am C-Eingang werden alle Bits um eine Position nach rechts verschoben. Nach 8 Zyklen ist ein Byte in dem 8-Bit-Register gespeichert (klickt auf die Zeichnung, um die Animation zu starten):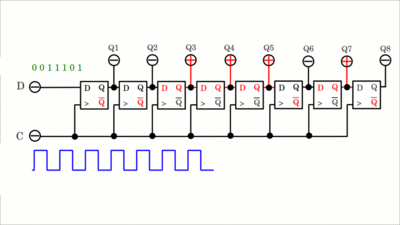

Abbildung 16: (Animation Starten)

Das Daten-Byte kann nach Abschluss des Schreibvorgangs im parallelen Modus an den Ausgängen Q1 bis Q8 ausgelesen werden. Dabei muss sichergestellt sein, dass der Lesevorgang nicht während des Schreibvorgangs ausgelöst wird, da man in diesem Fall falsche Daten erhält. Um eine Änderung der Daten am parallelen Ausgang während der Schreiboperation zu verhindern, kann ein Puffer zu dem Schaltkreis hinzugefügt werden (siehe weiter unten).
Der Schaltkreis ist ein Serial-In, Parallel-out (SIPO) Register.
Wird das Register durch ein Taktsignal angesteuert, kann die gespeicherte Information auch am Ausgang Q8 des rechten Flipflops gelesen werden (Serial-In, Serial-out Modus, SISO). Mit jedem Takt wird das Bit an diesem Flipflop herausgeschoben und verworfen, weshalb dieser Lesemodus im Englischen als destructive readout (zerstörendes Lesen) bezeichnet wird. Klickt auf die Zeichnung, um die Animation zu starten: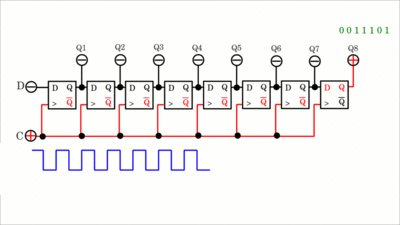

Animierte Zeichnung Shift Register destructive readout

Abbildung 17: (Animation Starten)

Die Schaltung eines Vielzweck 3-Bit-Registers ist deutlich komplexer (klickt auf die Zeichnung, um die Animation zu starten):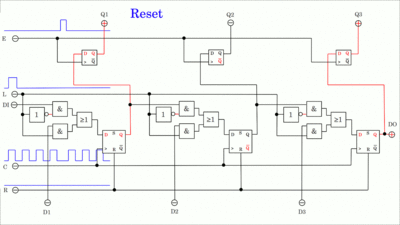

Animierte Zeichnung Vielzweck 3-Bit-Register

Abbildung 18: (Animation Starten)

Das Register kann in verschiedenen Modi betrieben werden:
Ist der Load-Eingang (L) deaktiviert (LOW), so arbeitet das Register im seriellen Modus, wobei Daten an DI (Data In) in die Speicherzellen geschrieben und mit jeder steigenden Flanke des Taktsignals um eine Position hin zum DO- (Data Out) Ausgang verschoben werden (SIPO-Modus).
Ein einzelner Puls am E- (Enable) Eingang kopiert den Status des Schieberegisters in den Ausgangspuffer und somit an die Ausgänge Q1 bis Q3 (SIPO-Modus).
Wird der L- (Load) Eingang aktiviert (HIGH), so wird der Status der Eingänge D1 bis D3 in das Schieberegister kopiert, sobald das Taktsignal (Clock, C) ansteigt. Ein einzelner Takt reicht zum Einlesen aus. (Parallel-In, Serial-Out PISO).
Ein einzelner Puls an den Reset- (R) Eingängen löscht den Speicher (alle Bits werden auf '0' gesetzt), was deutlich schneller geht, als drei Nullen im seriellen Modus zu schreiben.
Der Schaltkreis kann auch im Modus Parallel-In, Parallel-Out PIPO betrieben werden.
Zusätzliche Flipflops können an den DO-Ausgang angeschlossen werden, um den Speicherplatz zu erweitern; eine Gesamtzahl von acht Flipflops ermöglicht die Speicherung eines Bytes.

Multiplexer

Eine Selektionsschaltung, auch Multiplexer, kurz MUX genannt, ist ein Schaltkreis der eines von mehreren Eingangssignalen auswählt und an eine einzelne Datenleitung weitergibt.
Unter Verwendung eines Multiplexers können mehrere Signale ein einzelnes Bauteil durchlaufen. Zum Beispiel besitzt ein Atmega8-Mikrokontroller einen einzigen Analog-zu-Digital-Wandler, jedoch kann dieser über einen Multiplexer mit bis zu 6 Eingangspins verbunden werden.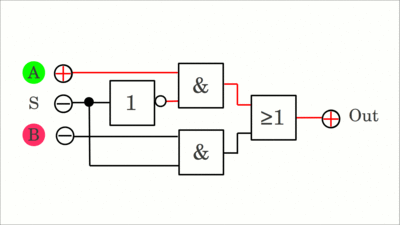

Abbildung 19: (Animation Starten)
Der hier gezeigte Multiplexer wurde bereits in dem Schaltkreis des Vielzweck-Schieberegisters weiter oben verwendet, um auszuwählen, ob der Speicher im seriellen oder parallelen Modus arbeitet.
Ist der S- (Select) Eingang deaktiviert (LOW), so wird Eingang A an den Ausgang weitergeleitet, während das Ausgangssignal Eingang B entspricht, wenn ein HIGH-Pegel anliegt. Klickt auf die Zeichnung, um die Animation zu starten.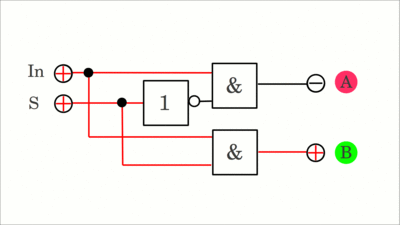

Abbildung 20: (Animation Starten)
Ein Demultiplexer, kurz Demux verteilt ein einzelnes Eingangssignal auf einen von mehreren Ausgängen. Bei dem hier gezeigten Schaltkreis wird der Eingang an Ausgang A weitergeleitet, wenn das Select-Signal auf LOW-Pegel ist. Ausgang B wird angewählt, wenn das Select-Signal auf HIGH-Pegel ist (klickt auf die Zeichnung, um die Animation zu starten). Der jeweils deaktivierte Ausgang bleibt auf LOW-Pegel.

Mit einem Multiplexer kann eines von mehreren Eingangssignalen zu einer einzelnen Datenleitung gesendet werden, während ein Demultiplexer verwendet werden kann, um das Eingangssignal auf einen von mehreren Ausgängen umzuleiten (klickt auf die Zeichnung, um die Animation zu starten):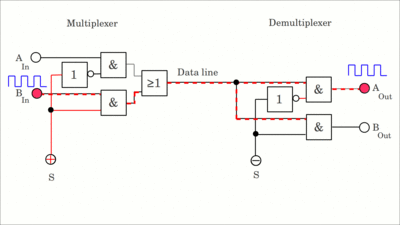

Animierte Zeichnung Multiplexer Demultiplexer

Abbildung 21: (Animation Starten)

Abbildung 22:
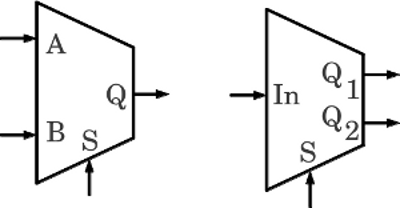
Schaltsymbole eines 2-in-1 Multiplexers (links) und eines 1-auf-2 Demultiplexers (rechts).

Zähler

Das JK-Flipflop ist dem zuvor gezeigten RS-Flipflop sehr ähnlich. Ist der J-Eingang auf HIGH-Pegel, während sich der K-Eingang auf LOW-Pegel befindet, "springt (jump)" Ausgang Q auf HIGH. Ist hingegen J auf LOW-Pegel und K auf HIGH-Pegel, so wird Ausgang Q "getötet (killed)". Sind beide Eingänge auf LOW-Pegel, so behält der Ausgang seinen Zustand bei (hold state). Sind beide Eingänge auf HIGH-Pegel, so nimmt das Ausgangssignal den komplementären Zustand zum aktuellen Status ein - das Signal schaltet um (engl.: toggle).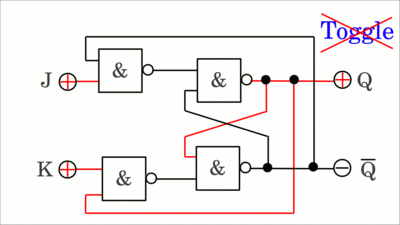

Abbildung 23: (Animation Starten)
Dieser vereinfachte Schaltkreis veranschaulicht die "Jump-" und "Kill-" Funktionalität, jedoch kann hiermit nicht der Vorgang des Toggelns gezeigt werden. Klickt auf die Zeichnung, um die Animation zu starten.

Der unten gezeigte Schaltkreis übernimmt die Signale am J- und K-Eingang während Eingang C auf HIGH-Pegel ist und setzt die Ausgänge an der fallenden Flanke des Clock-Signals. Ist J=K=HIGH, so wechselt der Ausgang seinen aktuellen Schaltzustand mit jedem Zyklus des Clock-Eingangs (klickt auf die Zeichnung, um die Arbeitsweise zu sehen):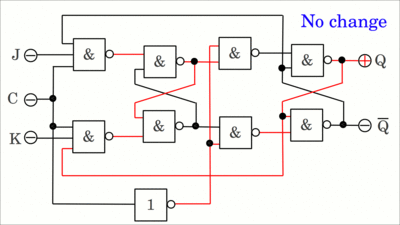

Abbildung 24: (Animation Starten)

Abbildung 25:
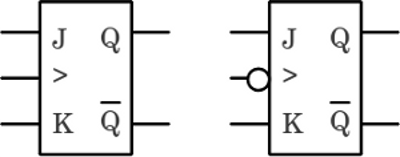
Die linke Seite zeigt das Schaltsymbol eines vorderflankengesteuerten JK-Flipflops, die rechte Seite die hinterflankengesteuerte Version.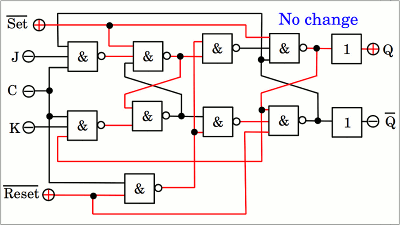

Abbildung 26:
JK -Flipflop mit "nicht Set" und "nicht Reset" Eingängen. Ist "nicht Set" auf LOW, so wird der Ausgang Q auf HIGH gesetzt, ist "nicht Reset" auf LOW, so wird Q auf LOW gesetzt. Normalerweise sind diese beiden Eingänge auf HIGH-Signal und sollten nie gleichzeitig auf LOW gesetzt werden.
An den Ausgängen befinden sich zusätzliche Puffer, die für die Funktion nicht notwendig sind, aber häufig eingesetzt werden, um die Ausgänge von den Eingängen zu trennen.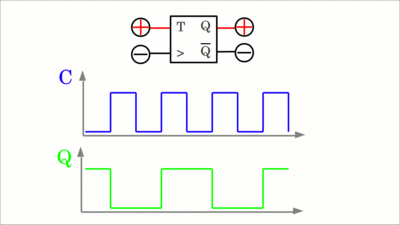

Abbildung 27: (Animation Starten)
Werden die Eingänge J und K miteinander verbunden, so erhält man ein T-Flipflop. Ist Eingang T (Toggle) auf LOW-Pegel, so behält der Ausgang seinen aktuellen Zustand bei, während das Ausgangssignal mit jedem Impuls am Clock-Eingang hin und her springt während Eingang T auf HIGH-Pegel ist.
Ein T-Flipflop teilt die Frequenz des Eingangssignals durch zwei.
Klickt auf die Zeichnung, um die Animation zu starten.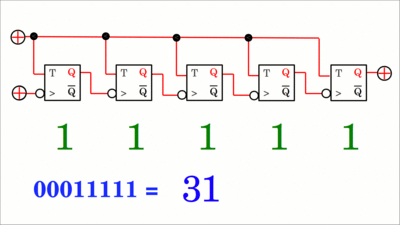

Abbildung 28: (Animation Starten)
Ordnet man mehrere hinterflankengesteuerte T-Flipflops in einer Reihe an, wobei der Ausgang Q des einen Flipflops mit dem T-Eingang des nächsten verbunden ist, so erhält man einen Zähler im Dualsystem. Das Eingangssignal ist mit dem C-Eingang des Flipflops ganz links verbunden und alle T-Eingänge sind auf HIGH-Pegel. Mit jeder fallenden Flanke des Eingangssignals wird die Dualzahl um eins erhöht.
Auch wenn die Animation (klickt auf die Zeichnung) vermuten lässt, dass alle Flipflops gleichzeitig ihren Zustand mit der fallenden Flanke des Eingangssignals wechseln, so gibt es durch jeden Baustein in der Kette eine leichte Verzögerung durch die jeweilige Gatterlaufzeit. Die Umschaltung erfolgt asynchron, weshalb es sich um einen asynchronen Zähler handelt, der bis 2ⁿ - 1 zählen kann, wobei n der Anzahl an Flipflops entspricht. Beachtet, dass das niederwertigste Bit der Dualzahl in dem Flipflop ganz links gespeichert wird.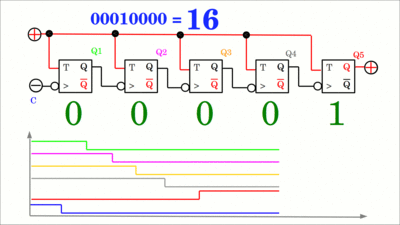

Abbildung 29: (Animation Starten)
Die Gatterlaufzeit jedes Flipflops wird in der Reihe des asynchronen Zählers aufaddiert während das Taktsignal den Schaltkreis in Richtung Q5 durchläuft. Die Animation (klickt auf die Zeichnung) zeigt den Übergang von 01111 (Dezimal 15) zu 10000 (Dezimal 16). Die Ausgänge schalten in einer "Wellenbewegung (engl.: ripple)" von links nach rechts, weshalb der Schaltkreis auch als ripple counter bezeichnet wird. Beachtet, dass sich das Least Significant Bit, also die niederwertigste Stelle auf der linken Seite befindet, während Dualzahlen üblicherweise mit dem LSB auf der rechten Seite geschrieben werden. Während das Taktsignal "durchgereicht" wird, werden kurzzeitig die falschen Zahlwerte 01110 (Dezimal 14), 01100 (Dezimal 12), 01000 (Dezimal 8) und 00000 (Dezimal 0) generiert. Da das "Durchreichen" sehr schnell geschieht, kann dieser Effekt in vielen Anwendungen vernachlässigt werden. Der Ripple-Effekt tritt an der fallenden Flanke des Taktsignals auf, womit eine einfache Lösung für das Problem darin besteht, den Leseprozess nur an der steigenden Flanke des Taktsignals zu starten.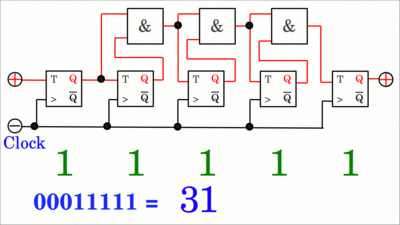

Abbildung 30: (Animation Starten)
Um einen Synchronzähler zu erhalten, muss das externe Taktsignal mit dem C-Eingang jedes Flipflops des Zählers verbunden sein, womit alle Flipflops ihren Schaltzustand gleichzeitig mit der steigenden Flanke des externen Takts wechseln. Durch Einfügen von UND-Gattern kann gesteuert werden, dass das jeweilige Flipflop seinen Schaltzustand nur ändert, wenn die Ausgänge aller vorherigen Flipflops auf HIGH-Pegel sind. In der Animation (klickt auf die Zeichnung) wechselt Flipflop Nummer eins ganz links mit jedem Puls des externen Taktsignals den Zustand seines Ausgangssignals, während Nummer zwei seinen Zustand nur ändert, wenn der Ausgang von Flipflop eins auf HIGH-Pegel ist. Nummer drei wechselt, wenn Flipflop eins UND zwei auf logisch HIGH sind, was durch das linke UND-Gatter sichergestellt wird und so weiter. Schließlich wechselt Flipflop Nummer fünf ganz rechts, welches die höchstwertige Stelle repräsentiert, nur dann seinen Zustand, wenn alle vier vorangeschalteten Flipflops auf logisch HIGH sind, was durch alle drei UND-Gatter in dem Schaltkreis sichergestellt wird.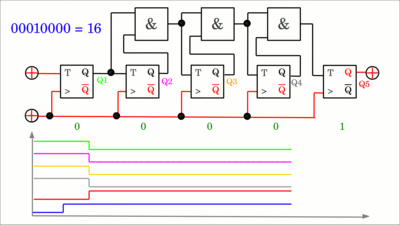

Abbildung 31: (Animation Starten)
Die Animation (klickt auf die Zeichnung) zeigt erneut den Übergang von 01111 (Dezimal 15) zu 10000 (Dezimal 16). Die Ausgänge aller fünf Flipflops wechseln gleichzeitig ihren Schaltzustand, womit die Gatterlaufzeit des Schaltkreises dem eines einzelnen Flipflops entspricht und es ist kein "Welleneffekt" zu beobachten. Die Gatterlaufzeit der UND-Gatter beeinflusst nicht die Laufzeitverzögerung an den Ausgängen des Zählers, jedoch die maximale Frequenz des externen Taktsignals. Der nächste Impuls sollte nicht gestartet werden, bevor alle Gatter ihren Endzustand entsprechend der Ausgangszustände aller Flipflops erreicht haben.

Addierer

Zwei Zahlen zu addieren, üblicherweise Dualzahlen, ist eine häufige Aufgabenstellung von Computern. Werden zwei einstellige Dualzahlen miteinander addiert, so sind die möglichen Ergebnisse:

	A		B		CS	Dezimal
1.)	0	+	0	=	0	0
2.)	0	+	1	=	1	1
3.)	1	+	0	=	1	1
4.)	1	+	1	=	10	2

Abbildung 32: (Animation Starten)
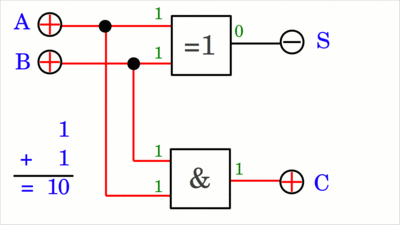
Die Addition kann durch ein AND- sowie ein XOR-Gatter verwirklicht werden (klickt auf die Zeichnung, um die Animation zu starten).
Die einstelligen Dualzahlen A und B werden addiert und das Ergebnis ist an den Ausgängen S (Sum, Summe) und C (Carry, übertragen) abzulesen. Das Carry-Signal repräsentiert einen Überlauf in die nächsthöhere Stelle. Der dezimale Wert der Summe errechnet sich zu: 2¹ * C + 2⁰ * S.

Der Speicher von Computern ist immer begrenzt. Ein 1-Bit-Register kann 2¹ = 2, ein 8-Bit-Register 2⁸ = 256 unterschiedliche Dualzahlen speichern. Ist das Ergebnis einer Berechnung größer als die maximale Zahl, die ein vorhandenes Register darstellen kann, so tritt die Überlauf-Bedingung (engl.: overflow) ein. Das Ergebnis von Fall Nummer 4 ist eine zweistellige Dualzahl, während die beiden Summanden einstellige Dualzahlen sind.

Abbildung 33: (Animation Starten)
Eine Addition kann durchgeführt werden, indem die beiden Summanden untereinander geschrieben und dann Spaltenweise, beginnend mit der rechten Spalte, addiert werden. Erzeugt das Ergebnis einer Teiladdition einen "Überlauf", d.h. das Ergebnis ist eine zweistellige Zahl, so wird die höherwertige Stelle auf die nächste Spalte übertragen. Diese Methode funktioniert nicht nur für Dezimalzahlen, sondern ebenfalls für Dualzahlen (klickt auf die Zeichnung, um die Animation zu starten).

Werden zwei Dualzahlen nach der Spaltenmethode addiert, so müssen bis zu drei einstellige Zahlen in einem Durchgang addiert werden. Die möglichen Resultate sind:

	A		B		C		CS	Dezimal
1.)	0	+	0	+	0	=	00	0
2.)	1	+	0	+	0	=	01	1
3.)	0	+	1	+	0	=	01	1
4.)	0	+	0	+	1	=	01	1
5.)	1	+	1	+	0	=	10	2
6.)	0	+	1	+	1	=	10	2
7.)	1	+	0	+	1	=	10	2
8.)	1	+	1	+	1	=	11	3

Abbildung 34: (Animation Starten)
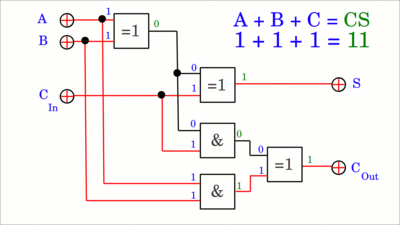
Einen elektronischen Schaltkreis, der die Addition von bis zu drei einstelligen Dualzahlen abbilden kann, nennt man einen Volladdierer (engl.: full adder). Bei der Addition zweier Dualzahlen kann ein Volladdierer den "Überlauf" der nächst niederwertigen Stelle einlesen und den "Überlauf" an den Volladdierer welcher die nächsthöhere Stelle repräsentiert, weiterleiten.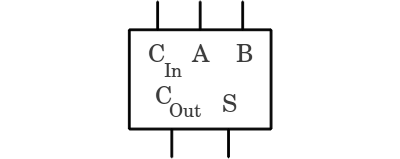

Abbildung 35:
Eingang A und B eines Volladdierers repräsentieren je eine einstellige Dualzahl. Der Carry-in Eingang ist mit dem Carry-out Ausgang des Volladdierers der nächst niederwertigen Stelle verbunden. Der Schaltkreis erzeugt eine zweistellige Dualzahl am Ausgang mit den Bezeichnungen S (Sum, Summe) und C_out (Carry-out, Übertrag).

Zwei mehrstellige Dualzahlen können aufaddiert werden, indem mehrere Volladdierer in Reihe geschaltet werden, wobei C_In mit C_Out der nächst niederwertigeren Stelle verbunden ist. Lediglich an der niederwertigsten Stelle ganz rechts genügt ein Halbaddierer. Hervorgerufen durch die Gatterlaufzeit wird das Carry-out-Signal verzögert an die nächsthöhere Stelle weitergeleitet und der Schaltkreis "rippelt" ähnlich dem Asynchronzähler, weshalb der hier zu sehende Addierer im Englischen auch als Ripple-Carry Adder bezeichnet wird.
Klickt auf die Zeichnung, um die Addition der Zahlen 175 und 165 zu sehen. Während der Berechnung werden auf Grund des Ripple-Effekts die falschen Zwischenergebnisse 266 und 320 produziert.
Beachtet, dass das Carry-Out-Bit der höchstwertigen Stelle nach der Addition gesetzt ist, was zeigt, dass das Ergebnis (340) zu groß für ein 8-Bit-Register ist.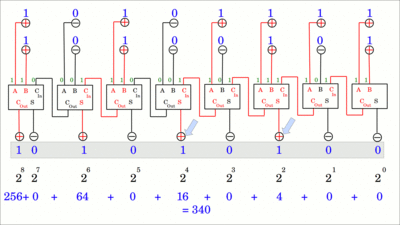

Abbildung 36: (Animation Starten)

Subtrahierer

Während bei der Addition zweier Zahlen unter Umständen die Überlauf-Bedingung auftritt, so kann das Ergebnis einer Subtraktion einen Wert kleiner als Null ergeben. In der elektronischen Datenverarbeitung repräsentieren unterschiedliche Datentypen unterschiedliche Zahlwerte. Eine vorzeichenlose 8-Bit Ganzzahl kann Werte von 0 bis 255 darstellen, während eine Vorzeichenbehaftete 8-Bit Ganzzahl Werte von -128 bis +127 repräsentiert. Bei der vorzeichenbehafteten Darstellung repräsentiert das Bit ganz links das jeweilige Vorzeichen. Der Wert ist negativ, wenn das am weitesten links stehende Bit 1 ist, da der Wert des höchstwertigen Bits bei der Umrechnung ins Dezimalsystem von der Summe aller niederwertigeren Bits abgezogen wird: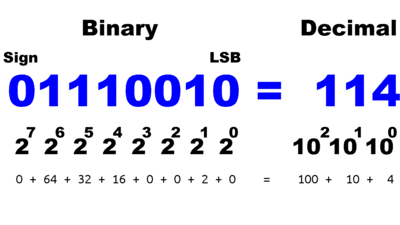

Abbildung 37: (Animation Starten)

Unter Beachtung der oben gezeigten Darstellung vorzeichenbehafteter Zahlen, die man als Zweierkomplement bezeichnet, wird aus der dezimalen Zahl +127 die 8-Bit-Dualzahl 0111111. Invertieren aller Stellen und Addieren von 1 ergibt: 10000000 + 1 = 100000001, also -127 im Dezimalsystem. Bedenkt, dass das höchstwertige Bit das Vorzeichen repräsentiert und dieses ist 1, also handelt es sich um eine negative Zahl.

Abbildung 38: (Animation Starten)
Generell kann eine Subtraktion nach folgendem Schema in eine Addition umgewandelt werden:

A - B = A + B + 1

Die Subtraktion von 17 - 97 kann in die Addition 17 +(-97) verwandelt werden, wofür 8-Bit Dualzahlen benötigt werden. Die Dualzahl 01100001 repräsentiert +97 im Dezimalsystem. Invertieren aller Stellen und Addieren von 1 ergibt: 10011110 + 1 = 10011111 was -97 im Dezimalsystem entspricht.
Das Ergebnis der nun folgenden Addition im Dualsystem lautet 10110010, was nach der Darstellung im Zweierkomplement der Dezimalzahl -80 entspricht. Klickt auf die Zeichnung, um die animierte Berechnung von 17 - 97 zu starten.

Der Ripple-carry adder kann in einen Ripple-carry subtractor verwandelt werden, indem XOR-Gatter an den B-Eingängen eingefügt und ein Volladdierer an der niederwertigsten Stelle verwendet wird. Ein weiteres XOR-Gatter wird mit dem Carry-out-Ausgang des höchstwertigen Volladdierers ganz rechts verbunden. Eingang M (Mode) steuert den Verwendungszweck des Schaltkreises. Ist M LOW, so ist das Carry-in-Signal des Volladdierers ganz links ebenfalls LOW und der Schaltkreis arbeitet als Addierer wie zuvor beschrieben. Ist M HIGH, so ist das Carry-in-Signal des rechten Volladdierers HIGH, womit zum Ergebnis eine 1 addiert wird. Je ein Eingang der XOR-Gatter wird auf HIGH-Pegel gebracht, womit die Bits von Register B an den Ausgängen der XOR-Gatter invertiert werden. Der Schaltkreis arbeitet als Subtrahierer (klickt auf die Zeichnung, um die Animation zu starten):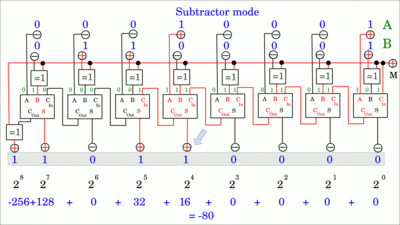

Abbildung 39: (Animation Starten)

Multiplikation kann durch wiederholte Addition umgesetzt werden: Zum Beispiel ist 3 multipliziert mit 7 gleichbedeutend mit der siebenfachen Addition von 3:
3 * 7 = 3 + 3 + 3 + 3 + 3 + 3 + 3 = 21
Beachtet die Überlaufbedingung nach jeder Addition! 17 multipliziert mit 100 erreicht die Überlaufbedingung nach 16 Zyklen, wenn vorzeichenlose 8-Bit-Ganzzahlen verwendet werden:
17 * 15 = 255, 17 * 16 = 272
Auch Division kann unter der Verwendung von Addition und Subtraktion umgesetzt werden. Die Division zweier Ganzzahlen kann jedoch mit einem "Restwert" enden, was zu einer weiteren Klasse von Zahlwerten in der elektronischen Datenverarbeitung führt: Fließkommazahlen, die jeweils eine Annäherung an reale Zahlen darstellen.
Den falschen Datentyp für eine mathematische Operation zu verwenden ist eine häufige Fehlerquelle beim Erstellen von Computersoftware.

Bau eigener Schaltkreise

Für die Schaltkreise in dem Video habe ich integrierte Logikgatter verwendet. Der Maximalstrom der verwendeten LEDs zur Visualisierung der Zustände der Ein-/Ausgänge beträgt etwa 30mA. Da der maximale Ausgangsstrom der Logikgatter unter diesem Wert liegt und ein Ausgang üblicherweise mehr als nur einen Eingang ansteuert, habe ich 560Ω Reihenwiderstände verwendet, um den Strom zu begrenzen. Bei einer Versorgungsspannung von 5V ist der Strom unter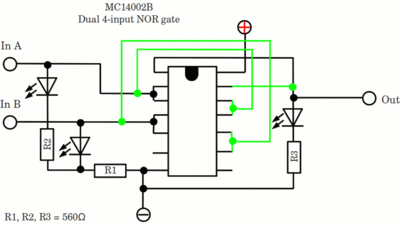 5V / 560Ω = 9mA.

Abbildung 40:
Die NOR-Gatter basieren auf CD4002BE Chips.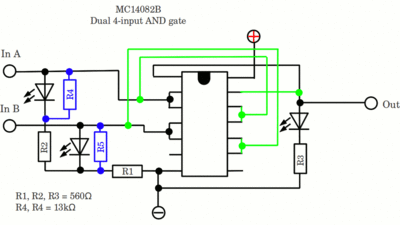

Abbildung 41:
Die UND-Gatter basieren auf HFC4082BE Chips.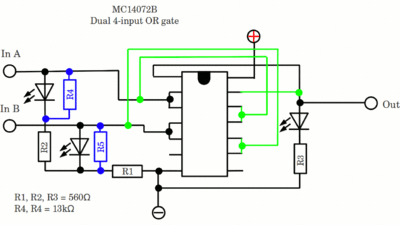

Abbildung 42:
Die OR-Gatter basieren auf CD4072BE Chips.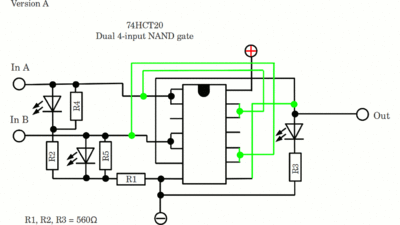

Abbildung 43:
Die NAND-Gatter basieren auf CD74HTC20 Chips.
Ich hatte Probleme mit den LOW-Leveln, weshalb ich zusätzliche 13kΩ-Widerstände parallel zu den LEDs an den Eingängen gelötet habe.
Version A:
Die Widerstands-LED Kombination ist parallel zu den Eingängen der Gatter gelötet, womit das HIGH-Signal der Versorgungsspannung entspricht (5V).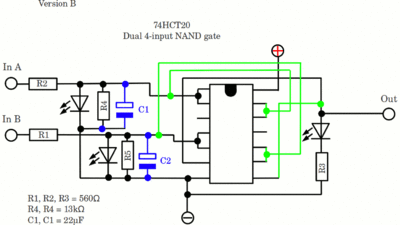

Abbildung 44:
Version B:
Nur die LED ist parallel zu dem jeweiligen Eingang geschaltet, der Serienwiderstand (R1 beziehungsweise R2) jedoch nicht, womit der HIGH-Pegel dem Spannungsabfall an der jeweiligen LED entspricht. Der Vorteil liegt darin, dass ein Kondensator parallel zur LED gelötet werden kann, womit ein Tiefpass entsteht (siehe das taktflankengesteuerte Flipflop im Video).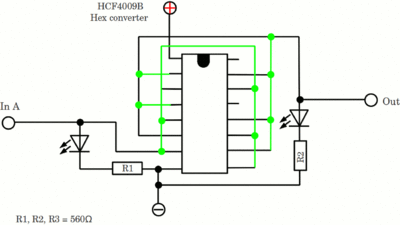

Abbildung 45:
Die NICHT-Gatter basieren auf HCF4009B Chips. Die grünen Linien zeigen optionale Verbindungen mit denen die Ein-/Ausgänge aller 6 Inverter auf dem Chip miteinander verbunden werden, um einen höheren Ausgangsstrom erzielen zu können. Da der Ausgangsstrom dieses Chips sehr gering ausfällt, sollten die grünen Verbindungen gesetzt werden.

<<< Logikgatter Relais >>>

Neuigkeiten Das Projekt Technik RoboSpatium Unterstützung Stichwortverzeichnis Archiv Download Reaktionen Spiele Verweise Gadgets Kontakt Impressum